정규성 검정 (Python)

728x90

정규성을 확인하는 방법은 시각적으로 표를 그려보는 방법, 통계 검정을 통해 확인하는 방법이 존재합니다.

시각화
1. Q-Q plot
통계 검정

정규성 검정을 설명하기 앞서, 정규성이란 어떤 것을 의미하는지 간단하게 확인할 필요가 있습니다.

따라서, 먼저 정규분포에 대해서 알아보자.

정규분포 (Nomal Distribution)

정규분포(Normal Distribution)는 Feature의 Value 분포를 그렸을 때, 중심(평균값)을 기준으로 좌우 대칭 형태로 나타나는 형태를 보인다. 육안으로는 Bell-Shape 형태를 따르는 것이다.
표준 정규분포(Standard normal distribution)는 평균이 0이고 표준 편차가 1인 분포를 얘기하며, z-분포라고 부르기도 한다.

이를 파이썬으로 그려보면, 다음과 같다.

# 라이브러리 호출
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(0)

# plot 스타일 지정
plt.style.use('default')
plt.rcParams['figure.figsize'] = (6, 3)
plt.rcParams['font.size'] = 12
plt.rcParams['lines.linewidth'] = 5

# 평균과 표준편차 선언
mu1, sigma1 = 0.0, 1.0
mu2, sigma2 = 1.5, 1.5
mu3, sigma3 = 3.0, 2.0

# x y 값 형성
x = np.linspace(-10, 10, 1000)
y1 = (1 / np.sqrt(2 * np.pi * sigma1**2)) * np.exp(-(x-mu1)**2 / (2 * sigma1**2))
y2 = (1 / np.sqrt(2 * np.pi * sigma2**2)) * np.exp(-(x-mu2)**2 / (2 * sigma2**2))
y3 = (1 / np.sqrt(2 * np.pi * sigma3**2)) * np.exp(-(x-mu3)**2 / (2 * sigma3**2))

# plot 그리기
plt.plot(x, y1, alpha=0.7, label=r'x~N(0, $1^2$)')
plt.plot(x, y2, alpha=0.7, label=r'x~N(1.5, $1.5^2$)')
plt.plot(x, y3, alpha=0.7, label=r'x~N(3.0, $2.0^2$)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.legend(bbox_to_anchor=(1.0, .2))
plt.show()

이러한 그래프로 도출되는 것을 정규분포라고 합니다. (그 중 파란색은 표준정규분포)

(참고)

2022.02.10 - [공부/통계학] - Distribution (분포도) python

Distribution (분포도) python

정규분포, 이항분포, t분포, 카이제곱분포 등 다양한 분포가 존재한다. 이번에는 파이썬을 활용하여 각 분포에 대해 그려보도록 한다. 정규분포 # 정규분포 그리는 함수 def normal_df(N, sigma, mu): #

signature95.tistory.com

데이터 값이 이런 정규분포를 따르는지 검정하는 법을 정규성 검정이라고 한다.

정규성을 확인하는 방법은 시각적으로 표를 그려보는 방법, 통계 검정을 통해 확인하는 방법이 존재합니다.

시각화 : Q-Q plot

통계 검정 : Shapiro - Test, Anderson - Test, KS - Test, Normal-Test, Jarque_bera - Test

시각화 (Q-Q Plot)

시각화하여 알아보게 된다면, 직관적이지만 P-value 값이 도출되지 않는다는 단점이 존재합니다.

자세한 설명은 여기를 참조하면 됩니다.

# 라이브러리 호출
from scipy.stats import probplot
import matplotlib.pyplot as plt 
import numpy as np 

np.random.seed(0)

n = 1000
x1 = np.random.normal(0, 10, n)
x2 = np.random.exponential(20, n)
x3 = np.log1p(x2)

# 시각화
f, axes = plt.subplots(2, 3, figsize=(12, 6))
axes[0][0].boxplot(x1)
probplot(x1, plot=axes[1][0])
axes[0][1].boxplot(x2)
probplot(x2, plot=axes[1][1])
axes[0][2].boxplot(x3)
probplot(x3, plot=axes[1][2])
plt.axis("equal")
plt.show()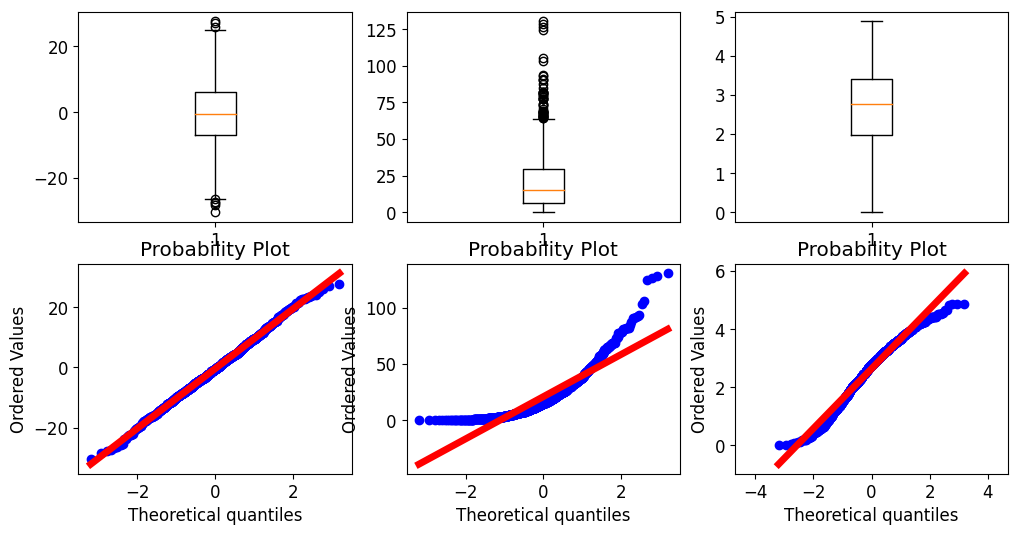

직관적이지만, 통계적 유의성 자체를 확인할 수 없는 단점이 큽니다. 따라서, 이번엔 통계 검정을 수행해보도록 합니다.

Shapiro - Test

- 귀무가설 : 해당 데이터가 정규성을 충족한다.
- 특징 : data수가 5000을 초과하는 경우, 정규성 검정에 대한 P 값을 담보하지 못한다. (즉, 통계적 유의성이 떨어진다.)

# 라이브러리 호출
import numpy as np
from scipy.stats import shapiro

# 정규분포를 따르도록 랜덤하게 값을 부여
np.random.seed(0)
n = 5000
x1 = np.random.normal(0, 100, n)

shapiro_test = stats.shapiro(x1)
shapiro_test

출력 결과

ShapiroResult(statistic=0.9997957944869995, pvalue=0.9398256540298462)

P값이 0.05(일반적인 귀무가설 검정 임계치 수준)보다 높기에, 해당 데이터는 정규성을 충족한다는 귀무가설을 유의하게 기각하지 못한다. 라고 해석할 수 있다.

X 데이터가 5000을 초과하는 경우,

# 라이브러리 호출
import numpy as np
from scipy.stats import shapiro

# 정규분포를 따르도록 랜덤하게 값을 부여
np.random.seed(1)
n = 5001
x2 = np.random.normal(0, 100, n)

shapiro_test = stats.shapiro(x2)
shapiro_test

출력 결과

/Library/Frameworks/Python.framework/Versions/3.9/lib/python3.9/site-packages/scipy/stats/morestats.py:1760: 
	UserWarning: p-value may not be accurate for N > 5000.
warnings.warn("p-value may not be accurate for N > 5000.")
ShapiroResult(statistic=0.9996199607849121, pvalue=0.46918171644210815)

Anderson - Test

- 귀무가설
특정 분포를 따른다. (특정 분포 : 'norm', 'expon', 'logistic', 'gumbel', 'gumbel_l', 'gumbel_r', 'extreme1'로 지정)
이때, 기본 값은 norm으로 정규분포를 따른다는 귀무가설을 검정한다. (참고로 extrame1, gumbel_l은 같은 분포를 의미함)

- 특징
1. 특정 분포를 따른다는 것을 검정할 수 있기에, 유용하게 사용할 수 있다. (모집단 자체의 분포를 알고 있다면, KS 검정보다 더 유용하게 사용할 수 있다)
2. 해당 분포를 검정할 때는 검정 통계치와 각 임계 값에 대한 통계치를 비교해야 한다.

# 라이브러리 호출
import numpy as np
from scipy.stats import anderson

# 데이터 형성
np.random.seed(0)
n = 10000
data = np.random.normal(size=n)

# Anderson-Darling Test 
anderson_result = anderson(data)

print(f'검정 통계치 : {anderson_result[0]}')
print(f'임계지점의 통계치 : {anderson_result[1]}')
print(f'각 임계 지점의 P-value : {anderson_result[2]}')

출력 결과

검정 통계치 : 0.31254017290666525
임계지점의 통계치 : [0.576 0.656 0.787 0.918 1.092]
각 임계 지점의 P-value : [15.  10.   5.   2.5  1. ]

P 값이 5.%일 때, 통계치보다 검정 통계치가 높게 나오기 때문에, 정규분포를 따른다는 귀무가설을 유의하게 기각하지 못한다라고 해석할 수 있다.

검정을 수행할 때는 다음과 같이 하면 된다. ( 참고 )

먼저, 정규성 검정이다.

# 라이브러리 호출
import numpy as np
from scipy.stats import anderson

# 데이터 형성
np.random.seed(0)
n = 10000
data = np.random.normal(size=n)

# Anderson-Darling Test 
anderson_result = anderson(data, dist='norm')

if anderson_result[0] < anderson_result[1][2]:
    print(f'해당 데이터의 검정 통계치 {round(anderson_result[0],3)}는 5% 유의수준 검정 통계치 {anderson_result[1][2]}보다 작다.\n따라서 정규분포를 따른다는 귀무가설을 기각할 수 없다.')
else:
    print(f'해당 데이터의 검정 통계치 {round(anderson_result[0],3)}는 5% 유의수준 검정 통계치 {anderson_result[1][2]}보다 크다.\n따라서 정규분포를 따른다는 귀무가설을 5%의 유의수준으로 기각할 수 있다.')

출력 결과

해당 데이터의 검정 통계치 0.313는 5% 유의수준 검정 통계치 0.787보다 작다.
따라서 정규분포를 따른다는 귀무가설을 기각할 수 없다.

그렇다면, 정규분포를 따르지 않는 경우는 어떨까? (카이제곱 분포를 따르는 데이터로 검정해본다)

# 라이브러리 호출
import numpy as np
from scipy.stats import anderson

# 데이터 형성 (카이제곱 분포를 따르는 10000개의 데이터)
np.random.seed(0)
n = 10000
data = np.random.chisquare(df=2, size=n)

# Anderson-Darling Test 
anderson_result = anderson(data, dist='norm')

if anderson_result[0] < anderson_result[1][2]:
    print(f'해당 데이터의 검정 통계치 {round(anderson_result[0],3)}는 5% 유의수준 검정 통계치 {anderson_result[1][2]}보다 작다.\n따라서 정규분포를 따른다는 귀무가설을 기각할 수 없다.')
else:
    print(f'해당 데이터의 검정 통계치 {round(anderson_result[0],3)}는 5% 유의수준 검정 통계치 {anderson_result[1][2]}보다 크다.\n따라서 정규분포를 따른다는 귀무가설을 5%의 유의수준으로 기각할 수 있다.')

출력 결과

해당 데이터의 검정 통계치 467.535는 5% 유의수준 검정 통계치 0.787보다 크다.
따라서 정규분포를 따른다는 귀무가설을 5%의 유의수준으로 기각할 수 있다.

KS-Test

- 귀무가설
2개 데이터의 분포가 동일하다. (2개의 sample에 대해서 분포가 다른지 검정하게 되는데, 1개의 데이터를 입력하고 'norm'을 입력해도 1개의 데이터가 정규분포를 따르는지 검정할 수 있다.)
- 특징
2개의 데이터에 대해 검정이 가능하기에, 두 데이터의 분포가 다른지 'two-sided', 'less', 'greater'을 사용하여 검정할 수 있다. (다양한 검정이 가능하다는 의미)
누적 확률 분포 (CDF)를 활용하여 특정 데이터의 분포가 모집단의 데이터 분포와 얼마나 유사한지 비교하거나, 두 데이터의 누적 확률 분포 차이를 비교한다.
KS 통계치는 즉, 누적 확률 분포 간 차이를 거리로 산정한 통계치이다.
조금 더 자세한 정보는 여기

# 라이브러리 호출
import numpy as np
from scipy.stats import kstest

# 정규분포를 따르도록 랜덤하게 값을 부여
x = np.random.normal(0,1,1000)

ks_test = stats.kstest(x , 'norm')
ks_test

출력 결과

KstestResult(statistic=0.03390269812637531, pvalue=0.19607426953777074)

P값이 0.19로 x가 정규분포와 동일하다는 귀무가설을 유의하게 기각하지 못한다. 따라서 x는 정규분포를 따른다고 해석할 수 있다.

Normal-Test

- 귀무가설
데이터가 정규분포를 따른다.
- 특징
왜도(skew)와 첨도(kurtosis)를 통해 정규성을 검정하게 된다. (검정 통계치 = s^2 + k^2)
검정하는 방식은 2-sided 카이제곱 검정으로 시행한다.

# 라이브러리 호출
import numpy as np
from scipy.stats import normaltest

# 정규분포를 따르도록 랜덤하게 값을 부여
np.random.seed(1)
n = 10000
x = np.random.normal(0, 500, n)

nn_test = stats.normaltest(x)
nn_test

출력 결과

NormaltestResult(statistic=1.412273027787057, pvalue=0.49354733198681766)

P값이 0.49로 x가 정규분포와 동일하다는 귀무가설을 유의하게 기각하지 못한다. 따라서 x는 정규분포를 따른다고 해석할 수 있다.

Jarque_bera - Test

- 귀무가설
데이터가 정규분포를 따른다.
- 특징
왜도(s)와 첨도(k)를 이용하여 정규성을 검정한다. 데이터 수가 충분히 큰 경우 (2000개를 초과)에 사용할 수 있다

참고 : JB 검정의 통계치는 다음과 같이 구할 수 있음.

# 라이브러리 호출
import numpy as np
from scipy.stats import jarque_bera

# 정규분포를 따르도록 랜덤하게 값을 부여
np.random.seed(2022)
n = 10000
x = np.random.normal(0, 500, n)

jb_test = stats.jarque_bera(x)
jb_test

출력 결과

Jarque_beraResult(statistic=0.8862949347952527, pvalue=0.6420125241904607)

P값이 0.64로 x가 정규분포와 동일하다는 귀무가설을 유의하게 기각하지 못한다. 따라서 x는 정규분포를 따른다고 해석할 수 있다.

728x90

저작자표시 비영리

'공부 > 통계학' 카테고리의 다른 글

웰치의 t 검정 : welch's t test (파이썬) (2)	2022.01.11
등분산 검정 (파이썬) (0)	2022.01.11
Chi-square-test (카이제곱검정) (0)	2021.11.18
T-test (T 검정) (0)	2021.11.17
로짓모형, 프로빗모형의 추정 (+최우법) (0)	2021.11.17

DataAnalyst

정규성 검정 (Python)

'공부 > 통계학' 카테고리의 다른 글

댓글

티스토리툴바

정규성 검정 (Python)

'공부 > 통계학' 카테고리의 다른 글

관련글

댓글

티스토리툴바