t 검정의 적용은 언제 하는 것일까?
https://ko.wikipedia.org/wiki/T-테스트
t-테스트 - 위키백과, 우리 모두의 백과사전
t-테스트(t-test) 또는 t-검정 또는 스튜던트 t-테스트(Student's t-test)는 검정통계량이 귀무가설 하에서 t-분포를 따르는 통계적 가설 검정법이다. t-테스트는 일반적으로 검정통계량이 정규 분포를
ko.wikipedia.org
t-테스트는 일반적으로 검정통계량이 정규 분포를 따르며 분포와 관련된 스케일링 변숫값들이 알려진 경우에 사용한다. 이 때 모집단의 분산과 같은 스케일링 항을 알 수 없으나 데이터를 기반으로 한 추정값으로 대체하면 검정통계량은 t-분포를 따른다. 예를 들어 t-테스트를 사용하여 두 데이터 세트(집단)의 평균이 서로 유의하게 다른지 여부를 판별 할 수 있다.
T-test의 기본 가정을 충족하는지 검정하는 부분은 다음 포스팅을 참고하시면 됩니다.
정규성 검정
2022.01.11 - [공부/모델링] - 정규성 검정 (Python)
정규성 검정 (Python)
정규성을 확인하는 방법은 시각적으로 표를 그려보는 방법, 통계 검정을 통해 확인하는 방법이 존재합니다. 시각화 Q-Q plot 통계 검정 Shapiro - Test Anderson - Test KS - Test Normal-Test Jarque_bera - Te..
signature95.tistory.com
등분산성 검정
2022.01.11 - [공부/모델링] - 등분산 검정 (파이썬)
등분산 검정 (파이썬)
등분산검정(Equal-variance test)은 두 정규성을 만족하는 데이터에서 생성된 두 개의 데이터 집합으로부터 두 정규분포의 모분산이 같은지 확인하기 위한 검정이다. 바틀렛(bartlett), 플리그너(fligner),
signature95.tistory.com
즉, 정규모집단에서 모평균을 검정할 때, 모분산이 알려지지 않은 경우에 사용하게 된다.
모분산이 알려지지 않은 경우라도 대표본 (n 이 30이상)인 경우는 z검정을 사용할 수 있다.
하지만, 소표본(n < 30)일 때 모분산을 모르는 경우, t분포를 이용해야 하며 모집단이 정규분포라는 가정이 반드시 동반된다.
모분산에 대한 정의는 동분산성으로 한다. (따라서, 이분산성이 의심되는 경우를 주의해야 한다.)
정리하자면 다음과 같다.
| 모평균 추정(모분산모름) + 표본이 30개 이상인 대표본인 경우 | Z - test 사용 |
| 모평균 추정(모분산모름) + 표본이 30개 미만인 소표본인 경우 | t - test 사용 (but, 모집단의 정규분포 가정이 동반됨) |
t 검정의 임계치
양측검정을 사용할 때,

단측검정을 이용할 때,

양측 검정을 사용하는 경우 : 두 집단의 평균이 다른 것을 검정하고 싶을 때 (두 집단의 평균에 차이가 있다)
단측 검정을 사용하는 경우 : 두 집단의 평균의 크기가 차이나는지 검정하고 싶을 때 (어느 집단의 평균이 크다, 작다)
"귀무가설은 차이가 없다. 대립가설은 차이가 존재한다." 로 설정할 수 있을 것이다. 따라서 임계치와 검정 통계량을 비교하여 가설을 검정할 수 있는 것이다.
t 검정을 위한 검정 통계량

참고)
재무비율을 이용한 부도예측에 대한 연구에서 T-test를 진행하였다.
부도와 정상기업인 2개 그룹에서 차이가 유의미한 재무비율 변수를 추출하는 데, 사용한 것이 T-test이다.
내가 생각했을때는,
2개 그룹의 특정 재무비율의 (평균)차이가 유의미한지 양측검정을 시행한 듯 하다.
"유의수준은 5%로 설정하여 신뢰수준 95%로 두 집단 간 특정 재무비율의 차이가 유의미하다고 할 수 있다"
라고 말 할 수 있는 재무비율을 추출한 것이 아닐까? 라는 생각이 든다.
하지만, 분명 기업의 수는 52000개에 육박한다. 물론 모집단에서 추출한 표본의 개수가 소표본이면 t-test를 사용한 것이 맞다는 생각이든다. 그래서 자료를 살펴보았다.
자료 내의 2003년도를 보면, 부도기업의 숫자가 32개밖에 되지 않는다. 따라서 표본을 추출하더라도 소표본이기 때문에, t-test를 진행했다는 생각을 하게 되었다.
물론 모집단의 분포가 정규분포를 따라야하지만, 여기서 n이 30이상이면 대표본으로서 정규성을 따른다고 보기 때문에 t-test의 가정을 충족할 수 있다는 생각이 들었다.
(예시 코드)
# 라이브러리 호출
import numpy as np
import scipy as sp
from matplotlib import rc
from scipy.stats import ttest_ind
import matplotlib.pyplot as plt
rc('font', family='AppleGothic')
plt.rcParams['axes.unicode_minus'] = False
# 이분산을 가지는 두 데이터 조건 형성
# 데이터 개수 500개, 분산은 등분산성, 평균의 차이
N1 = 500
N2 = 500
sigma_1 = 1
sigma_2 = 1
mu_1 = 5
mu_2 = 10
# 데이터 형성
np.random.seed(0)
x1 = sp.stats.norm(mu_1, sigma_1).rvs(N1)
x2 = sp.stats.norm(mu_2, sigma_2).rvs(N2)
# 시각화
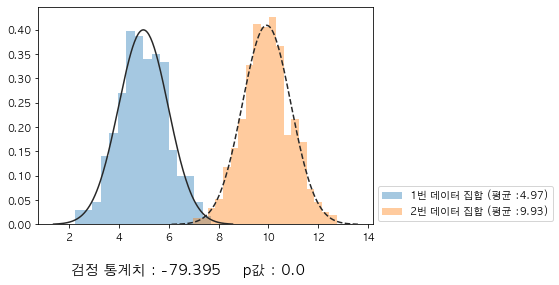
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label=f"1번 데이터 집합 (평균 :{np.round(x1.mean(),2)})")
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label=f"2번 데이터 집합 (평균 :{np.round(x2.mean(),2)})")
ax.lines[1].set_linestyle('--')
plt.legend(bbox_to_anchor=(1.0, .2))
plt.text(.2, -0.05, f'검정 통계치 : {np.round(ttest_ind(x1, x2)[0],3)} p값 : {ttest_ind(x1, x2)[1]}', fontsize=14, transform=plt.gcf().transFigure)
plt.show()출력 결과
참고)
t 분포 시각화 포스트
2022.02.10 - [공부/통계학] - Distribution (분포도) python
Distribution (분포도) python
정규분포, 이항분포, t분포, 카이제곱분포 등 다양한 분포가 존재한다. 이번에는 파이썬을 활용하여 각 분포에 대해 그려보도록 한다. 정규분포 # 정규분포 그리는 함수 def normal_df(N, sigma, mu): #
signature95.tistory.com
'공부 > 통계학' 카테고리의 다른 글
| 등분산 검정 (파이썬) (0) | 2022.01.11 |
|---|---|
| 정규성 검정 (Python) (0) | 2022.01.11 |
| Chi-square-test (카이제곱검정) (0) | 2021.11.18 |
| 로짓모형, 프로빗모형의 추정 (+최우법) (0) | 2021.11.17 |
| 로짓분석 (0) | 2021.11.16 |




댓글