웰치의 t 검정은 정규분포를 따르지만, 이분산성을 가지는 데이터에 대해 t-test를 진행하는 것이다.
이를 시행하려면, 정규성 검정과 등분산성 검정을 시행해야한다.
이전 글 참고
2022.01.11 - [공부/모델링] - 정규성 검정 (Python)
정규성 검정 (Python)
정규성을 확인하는 방법은 시각적으로 표를 그려보는 방법, 통계 검정을 통해 확인하는 방법이 존재합니다. 시각화 Q-Q plot 통계 검정 Shapiro - Test Anderson - Test KS - Test Normal-Test Jarque_bera - Te..
signature95.tistory.com
2022.01.11 - [공부/모델링] - 등분산 검정 (파이썬)
등분산 검정 (파이썬)
등분산검정(Equal-variance test)은 두 정규성을 만족하는 데이터에서 생성된 두 개의 데이터 집합으로부터 두 정규분포의 모분산이 같은지 확인하기 위한 검정이다. 바틀렛(bartlett), 플리그너(fligner),
signature95.tistory.com
먼저 평균의 차이가 존재하는 정규분포 데이터를 생성하고 분산도 다르게 설정한다.
# 라이브러리 호출
import numpy as np
import scipy as sp
from matplotlib import rc
import matplotlib.pyplot as plt
import seaborn as sns
rc('font', family='AppleGothic')
plt.rcParams['axes.unicode_minus'] = False
# 이분산을 가지는 두 데이터 조건 형성
# 데이터 개수 500개, 분산은 이분산성, 평균도 다르게 설정
N1 = 500
N2 = 500
sigma_1 = 1
sigma_2 = 4
mu_1 = 10
mu_2 = 20
# 랜덤데이터 형성 (정규분포)
np.random.seed(0)
x1 = sp.stats.norm(mu_1, sigma_1).rvs(N1)
x2 = sp.stats.norm(mu_2, sigma_2).rvs(N2)
# 시각화
ax = sns.distplot(x1, kde=False, fit=sp.stats.norm, label=f"1번 데이터 집합 (분산 :{np.round(x1.std(),3)})")
ax = sns.distplot(x2, kde=False, fit=sp.stats.norm, label=f"2번 데이터 집합 (분산 :{np.round(x2.std(),3)})")
ax.lines[1].set_linestyle('--')
plt.legend(bbox_to_anchor=(1.0, .2))
plt.show()출력 결과
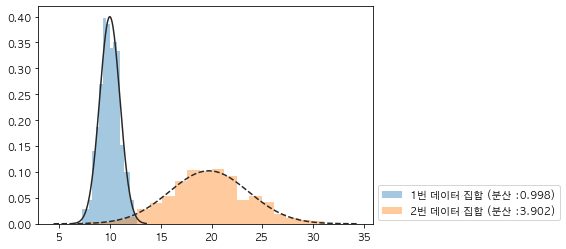
이를 확인하면, 평균과 분산이 육안으로도 유의하게 차이가 나는 것을 확인할 수 있다.
그렇다면, welch's t-test를 진행해보자.
from scipy.stats import ttest_ind
# welch's T-test 시행
print(f'검정 통계치 : {np.round(ttest_ind(x1, x2, equal_var = False)[0],3)}\np값 : {ttest_ind(x1, x2, equal_var = False)[1]}')출력 결과
검정 통계치 : -54.164
p값 : 1.1683096037126887e-225해석하자면, 2 모집단간 평균의 차이가 동일하다는 귀무가설을 매우 유의하게 기각할 수 있음을 확인할 수 있다.
더 나아가자면, ttest_ind에는 다양한 옵션도 존재한다.
다음은, scipy 라이브러리의 stats 매서드 내 ttest_ind에 대한 내용이다.
def ttest_ind(a, b, axis=0, equal_var=True, nan_policy='propagate',
permutations=None, random_state=None, alternative="two-sided",
trim=0):
"""
Calculate the T-test for the means of *two independent* samples of scores.
This is a two-sided test for the null hypothesis that 2 independent samples
have identical average (expected) values. This test assumes that the
populations have identical variances by default.
Parameters
----------
a, b : array_like
The arrays must have the same shape, except in the dimension
corresponding to `axis` (the first, by default).
axis : int or None, optional
Axis along which to compute test. If None, compute over the whole
arrays, `a`, and `b`.
equal_var : bool, optional
If True (default), perform a standard independent 2 sample test
that assumes equal population variances [1]_.
If False, perform Welch's t-test, which does not assume equal
population variance [2]_.
.. versionadded:: 0.11.0
nan_policy : {'propagate', 'raise', 'omit'}, optional
Defines how to handle when input contains nan.
The following options are available (default is 'propagate'):
* 'propagate': returns nan
* 'raise': throws an error
* 'omit': performs the calculations ignoring nan values
The 'omit' option is not currently available for permutation tests or
one-sided asympyotic tests.
permutations : non-negative int, np.inf, or None (default), optional
If 0 or None (default), use the t-distribution to calculate p-values.
Otherwise, `permutations` is the number of random permutations that
will be used to estimate p-values using a permutation test. If
`permutations` equals or exceeds the number of distinct partitions of
the pooled data, an exact test is performed instead (i.e. each
distinct partition is used exactly once). See Notes for details.
.. versionadded:: 1.7.0
random_state : {None, int, `numpy.random.Generator`,
`numpy.random.RandomState`}, optional
If `seed` is None (or `np.random`), the `numpy.random.RandomState`
singleton is used.
If `seed` is an int, a new ``RandomState`` instance is used,
seeded with `seed`.
If `seed` is already a ``Generator`` or ``RandomState`` instance then
that instance is used.
Pseudorandom number generator state used to generate permutations
(used only when `permutations` is not None).
.. versionadded:: 1.7.0
alternative : {'two-sided', 'less', 'greater'}, optional
Defines the alternative hypothesis.
The following options are available (default is 'two-sided'):
* 'two-sided'
* 'less': one-sided
* 'greater': one-sided
.. versionadded:: 1.6.0
trim : float, optional
If nonzero, performs a trimmed (Yuen's) t-test.
Defines the fraction of elements to be trimmed from each end of the
input samples. If 0 (default), no elements will be trimmed from either
side. The number of trimmed elements from each tail is the floor of the
trim times the number of elements. Valid range is [0, .5).
중요
1. equl_var를 설정하여 등분산, 이분산을 구분할 수 있다.
2. alternative를 통해 양측, 단측 검정을 사용할 수 있다.- 양측검정은 평균의 차이 자체를 검정하는 것이고, 단측은 평균이 크거나 작다는 것을 검정하는 것
추가)
scipy 사이트 링크
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html
scipy.stats.ttest_ind — SciPy v1.7.1 Manual
Yuen, Karen K., and W. J. Dixon. “The Approximate Behaviour and Performance of the Two-Sample Trimmed t.” Biometrika, vol. 60, no. 2, 1973, pp. 369-374. JSTOR, www.jstor.org/stable/2334550. Accessed 30 Mar. 2021.
docs.scipy.org
'공부 > 통계학' 카테고리의 다른 글
| VIF (분산확장요인, python) (0) | 2022.01.11 |
|---|---|
| 비모수 검정 : Mann-Witney U-test (만 - 위트니 U 검정, python) (0) | 2022.01.11 |
| 등분산 검정 (파이썬) (0) | 2022.01.11 |
| 정규성 검정 (Python) (0) | 2022.01.11 |
| Chi-square-test (카이제곱검정) (0) | 2021.11.18 |




댓글