이전 포스트에 이어서 작성하는 내용입니다.
2022.04.01 - [공부/통계학] - 선형회귀 분석1 (결정계수 구하기) python
선형회귀 분석1 (결정계수 구하기) python
이번 포스트에서는 단순선형회귀 summary를 통해 도출된 결정계수, 회귀계수, 회귀계수의 표준편차, 회귀계수의 T값 등의 의미와 직접 구하는 방법을 알아보고자 합니다. 일반적인 OLS를 파이썬에
signature95.tistory.com
앞선 포스트에서는 결정계수에 대해서 알아보았는데, 이번에는 회귀계수에 대해 알아보고자 합니다.
선형회귀에서 회귀계수는 최소제곱법을 통해서 도출하는데, 잔차를 최소화하는 방식으로 진행됩니다.
여기서 잔차를 식으로 표현하면 다음과 같습니다.

위 식에서 우리는 y_hat이 x와 ß로 표현가능한 회귀식임을 알 수 있습니다. 따라서 이를 다시 쓰면 다음과 같습니다.

즉, 잔차의 제곱합은 ß1, ß2에 대한 식임을 알 수 있습니다. 그럼 이를 ß에 대해 편미분하게 된다면 두개의 식을 도출할 수 있습니다. 또한 회귀계수에 대해 잔차 제곱합이 최소가 되는 지점을 찾아야하기에 편미분 = 0으로 설정하고 식을 풀어나가면 됩니다.


그리고 이 두 식을 다시 쓰면 다음과 같습니다.


위 두 식을 연립방적식을 통해 풀게되면 ß2는 다음과 같이 나옵니다.


이를 다시 풀어서 쓰면 다음과 같습니다.

여기서 X bar는 X의 표본평균을 의미하고 소문자 x는 평균값으로부터의 편차를 의미합니다.
다시 돌아와서 저번과 같이 boston 집값 데이터를 활용하여 이번에도 회귀계수를 직접 구해보고, statsmodels의 OLS 결과 값이랑 비교해보도록 하겠습니다.
먼저 OLS 결과 값입니다.
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.484
Model: OLS Adj. R-squared: 0.483
Method: Least Squares F-statistic: 471.8
Date: Fri, 01 Apr 2022 Prob (F-statistic): 2.49e-74
Time: 13:49:26 Log-Likelihood: -1673.1
No. Observations: 506 AIC: 3350.
Df Residuals: 504 BIC: 3359.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -34.6706 2.650 -13.084 0.000 -39.877 -29.465
RM 9.1021 0.419 21.722 0.000 8.279 9.925
==============================================================================
Omnibus: 102.585 Durbin-Watson: 0.684
Prob(Omnibus): 0.000 Jarque-Bera (JB): 612.449
Skew: 0.726 Prob(JB): 1.02e-133
Kurtosis: 8.190 Cond. No. 58.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
RM의 회귀계수가 9.1021인 것을 확인할 수 있습니다.
직접 구하는 코드는 다음과 같습니다.
# 회귀계수
y = np.array(target_array - target_array.mean())
x = np.array(feature['RM'] - feature['RM'].mean())
beta = np.sum(x * y) / np.sum(x **2)
print(f'매서드로 구한 회귀계수 coef \u03B2 : {model.params[1] : .5f}')
print(f'직접 구한 회귀계수 coef \u03B2 : { beta : .5f}')
>>>
매서드로 구한 회귀계수 coef β : 9.10211
직접 구한 회귀계수 coef β : 9.10211
numpy를 사용하여 이를 도출하였고, 위 식과 같은 형태로 beta를 구한 것을 확인할 수 있습니다.
그렇다면 이번에는 beta의 표준편차를 구해보도록 하겠습니다.
표준편차의 식은 다음과 같습니다.

여기서 분자는 시그마로 분산을 의미합니다. 정확히는 잔차의 분산입니다. 참고로 잔차의 분산은 잔차의 제곱을 잔차의 자유도로 나누면 됩니다. 따라서 이를 코드로 구현하면 다음과 같습니다.
# 회귀계수의 표준편차
var_error = np.sum((model.resid) ** 2) / model.df_resid
deviation_x = np.sum((feature['RM'] - feature['RM'].mean()) ** 2)
std_beta = (var_error/deviation_x) ** 0.5
print(f'매서드로 구한 회귀계수의 표준편차 se(\u03B2) : {model.cov_params()["RM"][1] ** 0.5 : .5f}')
print(f'직접 구한 회귀계수의 표준편차 se(\u03B2) : { std_beta : .5f}')
>>>
매서드로 구한 회귀계수의 표준편차 se(β) : 0.41903
직접 구한 회귀계수의 표준편차 se(β) : 0.41903
그렇다면, 마지막으로는 회귀계수의 t값에 대해 구해보고자 합니다. t값을 통해 회귀계수의 통계적 유의성을 확인할 수 있는데, 보통 t가 2를 넘는 경우 p값이 유의한 것으로 도출됩니다.
먼저 t값을 표현하면 다음과 같습니다.
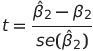
여기서 미지의 ß2를 포함하는 신뢰구간은 다음과 같습니다.
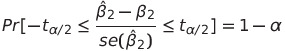
그리고 귀무가설은 ß2 hat = ß2 라고 할 수 있습니다. 이를 ß2 hat에 대해 쓰면 다음과 같이 정리할 수 있습니다.

이는 귀무가설이 성립할때, 회귀계수 추정치가 포함될 확률이 1 - alpha인 구간이라 할 수 있습니다. 여기서 신뢰구간은 귀무가설의 채택영역이며 신뢰구간 밖의 구간을 기각역이라고 합니다. 그리고 신뢰구간의 양 극단을 임계치라고 합니다.
다시 돌아와서 보면, 우리는 귀무가설이 성립할 때의 t값을 회귀계수/회귀계수의 표준편차로 구할 수 있을 것입니다.
이를 코드로 보면 다음과 같습니다.
# 회귀계수의 t값
t_beta = beta/std_beta
print(f'매서드로 구한 회귀계수(\u03B2)의 t값 : {model.tvalues[1] : .5f}')
print(f'직접 구한 회귀계수(\u03B2)의 t값 : { t_beta : .5f}')
>>>
매서드로 구한 회귀계수(β)의 t값 : 21.72203
직접 구한 회귀계수(β)의 t값 : 21.72203
'공부 > 통계학' 카테고리의 다른 글
| 구조변화 검정 (Chow-test) python (0) | 2022.04.08 |
|---|---|
| AR(p) 모형 (0) | 2022.04.06 |
| 선형회귀 분석1 (결정계수 구하기) python (0) | 2022.04.01 |
| Monte Carlo simulation (몬테카를로 시뮬레이션) python (0) | 2022.03.28 |
| 선형회귀 기초 (0) | 2022.03.24 |




댓글