이번 포스트에서는 단순선형회귀 summary를 통해 도출된 결정계수, 회귀계수, 회귀계수의 표준편차, 회귀계수의 T값 등의 의미와 직접 구하는 방법을 알아보고자 합니다.
일반적인 OLS를 파이썬에서 수행하려면 다양한 라이브러리가 있지만, summary를 통해 OLS 결과를 종합적으로 도출해주는 statsmodels 라이브러리로 이번 파트를 알아보도록 하겠습니다.
먼저 데이터는 보스턴 집값 데이터를 불러오도록 합니다.
import pandas as pd
from sklearn.datasets import load_boston
# 데이터셋 불러오기
housing = load_boston()
# feature, target 데이터 설정
feature = pd.DataFrame(housing.data, columns=housing.feature_names)
target = pd.DataFrame(housing.target, columns=['MEDV'])
단순선형 회귀모형을 도출할 것이기 때문에, 변수를 하나 추출하는데 여기서 target과 양의 상관계수가 가장 높은 컬럼을 선정해보겠습니다.
total = pd.concat([feature,target], axis=1)
total.corr()
>>>
CRIM ZN INDUS CHAS NOX RM AGE \
CRIM 1.000000 -0.200469 0.406583 -0.055892 0.420972 -0.219247 0.352734
ZN -0.200469 1.000000 -0.533828 -0.042697 -0.516604 0.311991 -0.569537
INDUS 0.406583 -0.533828 1.000000 0.062938 0.763651 -0.391676 0.644779
CHAS -0.055892 -0.042697 0.062938 1.000000 0.091203 0.091251 0.086518
NOX 0.420972 -0.516604 0.763651 0.091203 1.000000 -0.302188 0.731470
RM -0.219247 0.311991 -0.391676 0.091251 -0.302188 1.000000 -0.240265
AGE 0.352734 -0.569537 0.644779 0.086518 0.731470 -0.240265 1.000000
DIS -0.379670 0.664408 -0.708027 -0.099176 -0.769230 0.205246 -0.747881
RAD 0.625505 -0.311948 0.595129 -0.007368 0.611441 -0.209847 0.456022
TAX 0.582764 -0.314563 0.720760 -0.035587 0.668023 -0.292048 0.506456
PTRATIO 0.289946 -0.391679 0.383248 -0.121515 0.188933 -0.355501 0.261515
B -0.385064 0.175520 -0.356977 0.048788 -0.380051 0.128069 -0.273534
LSTAT 0.455621 -0.412995 0.603800 -0.053929 0.590879 -0.613808 0.602339
MEDV -0.388305 0.360445 -0.483725 0.175260 -0.427321 0.695360 -0.376955
DIS RAD TAX PTRATIO B LSTAT MEDV
CRIM -0.379670 0.625505 0.582764 0.289946 -0.385064 0.455621 -0.388305
ZN 0.664408 -0.311948 -0.314563 -0.391679 0.175520 -0.412995 0.360445
INDUS -0.708027 0.595129 0.720760 0.383248 -0.356977 0.603800 -0.483725
CHAS -0.099176 -0.007368 -0.035587 -0.121515 0.048788 -0.053929 0.175260
NOX -0.769230 0.611441 0.668023 0.188933 -0.380051 0.590879 -0.427321
RM 0.205246 -0.209847 -0.292048 -0.355501 0.128069 -0.613808 0.695360
AGE -0.747881 0.456022 0.506456 0.261515 -0.273534 0.602339 -0.376955
DIS 1.000000 -0.494588 -0.534432 -0.232471 0.291512 -0.496996 0.249929
RAD -0.494588 1.000000 0.910228 0.464741 -0.444413 0.488676 -0.381626
TAX -0.534432 0.910228 1.000000 0.460853 -0.441808 0.543993 -0.468536
PTRATIO -0.232471 0.464741 0.460853 1.000000 -0.177383 0.374044 -0.507787
B 0.291512 -0.444413 -0.441808 -0.177383 1.000000 -0.366087 0.333461
LSTAT -0.496996 0.488676 0.543993 0.374044 -0.366087 1.000000 -0.737663
MEDV 0.249929 -0.381626 -0.468536 -0.507787 0.333461 -0.737663 1.000000
확인해보면, RM(room number 방의 개수)과 MEDV(본인 소유 주택의 중앙값 : 단위 1000)가 가장 높은 양의 상관성을 가지는 것을 알 수 있습니다.
이를 seaborn의 pairplot으로 그리면 다음과 같이 나옵니다.
import matplotlib.pyplot as plt
import seaborn as sns
sns.pairplot(pd.concat([feature['RM'], target], axis= 1), kind='reg')
그렇다면, 이번엔 두 데이터에 대해 단순 선형회귀를 statsmodels로 구현해보겠습니다.
import statsmodels.api as sm
model = sm.OLS(target, sm.add_constant(feature['RM'])).fit()
model.summary()
>>>
OLS Regression Results
==============================================================================
Dep. Variable: MEDV R-squared: 0.484
Model: OLS Adj. R-squared: 0.483
Method: Least Squares F-statistic: 471.8
Date: Fri, 01 Apr 2022 Prob (F-statistic): 2.49e-74
Time: 00:44:54 Log-Likelihood: -1673.1
No. Observations: 506 AIC: 3350.
Df Residuals: 504 BIC: 3359.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -34.6706 2.650 -13.084 0.000 -39.877 -29.465
RM 9.1021 0.419 21.722 0.000 8.279 9.925
==============================================================================
Omnibus: 102.585 Durbin-Watson: 0.684
Prob(Omnibus): 0.000 Jarque-Bera (JB): 612.449
Skew: 0.726 Prob(JB): 1.02e-133
Kurtosis: 8.190 Cond. No. 58.4
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
RM의 회귀계수는 9.1021로 나옵니다. 이는 해석하면, 방이 하나 늘어날때 마다 집 값이 9102.1$ (=9.1021 * 1000$)만큼 증가한다는 것을 의미합니다.
이를 시각화하면 다음과 같습니다.
# 회귀선 도출
target_pred = model.predict()
plt.scatter(feature['RM'], target, marker='+', label='$MEDV_i$ 실제 관측치')
plt.plot(feature['RM'], target_pred, color = 'g', label='$\hat{MEDV}_i$ 회귀선')
plt.hlines(target.mean(), feature['RM'].min(), feature['RM'].max(), color = 'r', label='$MEDV_i$ 평균선')
plt.legend()
plt.xlabel('RM : Room number')
plt.ylabel('MEDV : Median value of owner-occupied homes')
plt.show()
그렇다면 다시 돌아와서 결정계수를 도출해보도록 하겠습니다.
먼저 결정계수는 다음과 같이 정의됩니다.
R^2 = SSR/SST = 1 -SSE/SST

- SST는 편차의 제곱으로서 위 그림에서는 빨간 선에 해당합니다. 또한 총변동을 의미합니다.
- SSR는 편차와 회귀선 값 차이의 제곱으로서 회귀식으로 설명이 가능한 변동을 의미하고 초록색 선에 해당합니다.
- SSE은 잔차의 제곱으로서 설명이 불가능한 변동을 의미하고 노란색 선에 해당합니다.
즉 결정계수는 총변동에서 (회귀식으로) 설명가능한 변동이 얼마나 되는지 알 수 있는 지표에 해당합니다. 만약 관측치가 회귀식 위에 모두 존재하게 된다면 결정계수는 1이됩니다. (다른말로 target, feature가 완전한 선형관계로서 상관계수가 1일 때를 의미)
그렇다면 직접 결정계수 값을 도출해보고 statsmodel의 summary에서 나온 결정계수 값과 비교해보겠습니다.
# 먼저 target 데이터를 array 형태로 새로 지정합니다. (pandas로 계속 하는 경우, str 오류 발생)
target_array = housing.target
# y_hat 도출
target_pred1 = model.predict()
# SST(편차의 제곱, 총변동), SSR(편차와 잔차의 차이 제곱 : 회귀식으로 설명가능한 변동), SSE(잔차의 제곱 : 회귀식으로 설명하지 못하는 변동)
SST = sum((target_array - target_array.mean()) ** 2)
SSR = sum((target_pred1 - target_array.mean()) ** 2)
SSE = sum((model.resid) ** 2)
r_squared = (1 - (SSE/SST))
print(f'매서드로 구한 결정계수 R-squared : {model.rsquared : .5f}')
print(f'직접 구한 결정계수 R-squared : {r_squared : .5f}')
>>>
매서드로 구한 결정계수 R-squared : 0.48353
직접 구한 결정계수 R-squared : 0.48353
즉 위 회귀식으로 설명할 수 있는 변동성은 48.353%라는 결과를 도출할 수 있습니다.
그렇다면 이번엔 조정된 결정계수 Adjusted R squared 값을 구해보도록 합니다.
조정된 결정계수는 feature가 많아지면 결정계수가 올라가는 점에 대해 규제항목을 추가한 형태입니다.
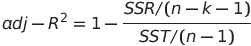
여기서 k는 feature의 개수이며 n은 관측치의 개수입니다.
따라서 이를 구해보면 다음과 같습니다.
n = model.nobs
k = 1
adj_r_squared = 1 - (SSE / (n - k - 1)) / (SST / (n - 1))
print(f'매서드로 구한 조정된 결정계수 Adj R-squared : {model.rsquared_adj : .5f}')
print(f'직접 구한 조정된 결정계수 Adj R-squared : {adj_r_squared : .5f}')
>>>
매서드로 구한 조정된 결정계수 Adj R-squared : 0.48250
직접 구한 조정된 결정계수 Adj R-squared : 0.48250
다음 포스트에서 회귀계수에 대해 이어집니다.
2022.04.01 - [공부/통계학] - 선형회귀 분석2 (회귀계수) python
선형회귀 분석2 (회귀계수) python
이전 포스트에 이어서 작성하는 내용입니다. 2022.04.01 - [공부/통계학] - 선형회귀 분석1 (결정계수 구하기) python 선형회귀 분석1 (결정계수 구하기) python 이번 포스트에서는 단순선형회귀 summary를
signature95.tistory.com
'공부 > 통계학' 카테고리의 다른 글
| AR(p) 모형 (0) | 2022.04.06 |
|---|---|
| 선형회귀 분석2 (회귀계수) python (0) | 2022.04.01 |
| Monte Carlo simulation (몬테카를로 시뮬레이션) python (0) | 2022.03.28 |
| 선형회귀 기초 (0) | 2022.03.24 |
| 로지스틱 회귀분석 (Logistic Regression) python (0) | 2022.02.21 |




댓글