이전포스트에 이어서 작성하는 내용입니다.
2022.03.25 - [공부/통계학] - 통계적 추론과 바람직한 추정량 python
통계적 추론과 바람직한 추정량 python
통계추론의 의미는 모집단으로부터의 표본에 근거하여 모집단에 대한 정보를 알아내는 과정이라 할 수 있습니다. 먼저 통계추론은 추정(estimation)과 가설검정(hypothesis testing)으로 구분되는데,
signature95.tistory.com
이번에는 지난 포스트에서 언급한 BLUE (Best Lenear Unbiased Estimator)의 특성을 몬테카를로 시뮬레이션으로 증명해보려 합니다.
몬테카를로 시뮬레이션은 표본추출 실험으로서 난수를 생성하여 소표본, 유한표본에서 추정량의 형태에 대해 연구하는데 유용하게 사용합니다.
이 방법을 이용한 가장 쉬운 방법이 구글링에서도 다수 등장하는데, 바로 원 넓이를 통한 원주율 π를 계산하는 법입니다.
먼저 코드로 한번 구현해보겠습니다. (참고로 tqdm은 for문 시행시 진행상황을 알 수 있는 라이브러리입니다)
from tqdm import tqdm
import pandas as pd
import numpy as np
# 변수 설정
n = 5000000
count = 0
x_list_under = []
y_list_under = []
x_list_upper = []
y_list_upper = []
for i in tqdm(range(n)):
# 시드 부여 (난수)
np.random.seed(i)
# 0,1 사이의 난수 값 생성
x = np.random.random()
y = np.random.random()
# 원 내부에 있는 점을 만족하는 경우, 그렇지 않은 경우 분리
if (x**2 + y**2) <= 1:
count += 1
x_list_under.append(x)
y_list_under.append(y)
else:
x_list_upper.append(x)
y_list_upper.append(y)
# 원 내부일 확률은 원 넓이의 1/4 이므로 곱하기 4로 π 계산
print('\u03C0 값', 4*count/n)
under = pd.DataFrame(zip(x_list_under,y_list_under), columns=['x_under', 'y_under'])
upper = pd.DataFrame(zip(x_list_upper,y_list_upper), columns=['x_upper', 'y_upper'])
plt.figure(figsize=(8,8))
plt.scatter(under['x_under'], under['y_under'], s=1)
plt.scatter(upper['x_upper'], upper['y_upper'], s=1)
plt.xlabel('x')
plt.ylabel('y')
plt.show()결과 값
100%|██████████| 5000000/5000000 [01:12<00:00, 68680.92it/s]
π 값 3.1423632
이처럼 몬테카를로 방법은 모수를 추정하는 통계적 연구가 이뤄지기도 하며 소표본, 유한표본에서 유용하게 사용합니다.
또한, 대표적인 사례로서 멘하탄 프로젝트에서도 이 기법을 사용하였고 현재 AI, DL(deep learning)등 다양한 분야에서 사용되고 있는 기법입니다.
그렇다면 다시 돌아와서 이 방법을 통해 BLUE를 실험적으로 증명해보도록 합니다.


먼저 위 처럼 임의의 모수와 샘플에 대해 값을 설정합니다. (임의의 모수로 b1 = 10, b2 =0.5)
import numpy as np
import matplotlib.pyplot as plt
# 시드 부여
np.random.seed(2022)
# 임의의 모수 값 지정
N = 100
beta_0 = 10
beta_1 = 0.5
# 샘플 데이터 형성
x = np.arange(start = 0, stop = N + 1, step = 1)
resid = np.random.normal(loc = 0, scale = 7, size = len(x))
y_hat = beta_0 + beta_1 * x + resid
y = beta_0 + beta_1 * x
이렇게 형성된 데이터 y, y_hat을 도표로 시각화 하면 다음과 같이 출력됩니다.
# 시각화
plt.figure(figsize = (10, 8))
plt.plot(x, y_hat, linestyle = "None", marker = "o", markerfacecolor = 'none')
plt.plot(x, y, linestyle = "dashed")
plt.show()
모회귀선을 기준으로 잔차가 분포하는 것을 확인할 수 있습니다.
그렇다면 이번엔 OLS회귀를 시행해봅니다.
import statsmodels.api as sm
# 회귀 분석 시행
model = sm.OLS(y_hat, sm.add_constant(x)).fit()
print(model.summary())
print(f'상수항(beta_0)의 추정 값 : {model.params[0]}')
print(f'회귀계수(beta_1)의 추정 값 : {model.params[1]}')결과값
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.818
Model: OLS Adj. R-squared: 0.816
Method: Least Squares F-statistic: 445.0
Date: Mon, 28 Mar 2022 Prob (F-statistic): 2.07e-38
Time: 00:55:23 Log-Likelihood: -334.42
No. Observations: 101 AIC: 672.8
Df Residuals: 99 BIC: 678.1
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 10.8020 1.324 8.161 0.000 8.176 13.428
x1 0.4824 0.023 21.096 0.000 0.437 0.528
==============================================================================
Omnibus: 2.273 Durbin-Watson: 1.857
Prob(Omnibus): 0.321 Jarque-Bera (JB): 1.804
Skew: -0.317 Prob(JB): 0.406
Kurtosis: 3.162 Cond. No. 115.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
상수항(beta_0)의 추정 값 : 10.801962306113486
회귀계수(beta_1)의 추정 값 : 0.4824340016142614
이런 형태로 난수를 생성하여 상수항과 회귀계수를 구할 수 있습니다.
그렇다면, 이런 과정을 수만번 시행하게 된다면, 모수의 값인 10, 0.5가 도출될 수 있는지 몬테카를로 방법을 시행해 보겠습니다.
# 라이브러리 호출
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from tqdm import tqdm
# 회귀계수 추정값 리스트 생성
beta_0_list = []
beta_1_list = []
# 몬테카를로 시뮬레이션 시행횟수 지정 (10만회)
simulation = 100000
# 임의의 모수 값 지정
beta_0 = 10
beta_1 = 0.5
# sample 데이터 개수 설정
N = 25
for i in tqdm(range(simulation)):
# 시드 부여
np.random.seed(i)
# 샘플 데이터 형성
x = np.arange(start = 0, stop = N + 1, step = 1)
resid = np.random.normal(loc = 0, scale = 7, size = len(x))
y_hat = beta_0 + beta_1 * x + resid
# 회귀 분석 시행
model = sm.OLS(y_hat, sm.add_constant(x)).fit()
# 회귀계수 추정치 리스트에 추가
beta_0_list.append(model.params[0])
beta_1_list.append(model.params[1])
print(f'상수항(beta_0)의 추정 값 : {np.mean(beta_0_list)}')
print(f'회귀계수(beta_1)의 추정 값 : {np.mean(beta_1_list)}')결과 값
100%|██████████| 100000/100000 [02:10<00:00, 764.63it/s]
상수항(beta_0)의 추정 값 : 9.989879731745281
회귀계수(beta_1)의 추정 값 : 0.5002362491438527
이처럼 몬테카를로 방법으로 최소제곱추정값이 불편추정량(Unbiased Estimator)인 것을 입증할 수 있습니다. 이는 고전적 선형회귀모형CLRM의 가정하에 다음과 같이 쓸 수 있습니다.
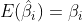
해석하면 표본을 통해 추출한 회귀계수 기대값이 곧 모수의 값과 일치한다는 것입니다.
참고로 간단하게 CLRM가정 7개를 언급하자면 다음과 같습니다.
- 선형회귀모형 (모수에 대해 선형성 존재)
- 오차항은 feature에 대해 독립성을 지님 ( COV(X_i, u_i)=0 )
- 오차항의 평균 = 0 ( E(u_i | X_i) = 0 )
- 오차항의 등분산성 ( var(u_i) = σ^2 ) : 등분산성 검정하는 법 (링크)
- 오차항의 자기상관성 X ( COV(u_i , u_j ) = 0 ) : 위배되는 경우 (링크)
- observatioin의 개수 n이 target 개수보다 많아야 함
- feature 관측치에 outlier(이상치)가 없어야 함
그렇다면 도출된 회귀계수와 상수항 ß1 ß0 를 시각화해보도록 해보고 마치도록 하겠습니다.
# beta_0 시각화
sns.distplot(beta_0_list, label='$\hat\u03B2_0$')
plt.vlines(x=beta_0, ymin=0, ymax=0.18, alpha = .5, colors='k', linestyles='dashed', label=f'$\u03B2_0$ = {beta_0}')
plt.vlines(x=np.mean(beta_0_list), ymin=0, ymax=0.20, alpha = .5 ,colors='r', linestyles='dotted', label=f'$\widebar\hat\u03B2_0$ = {np.mean(beta_0_list) : .3f}')
plt.title(r'$\hat \beta_{0}$의 분포도')
plt.xlabel(r'$\hat \beta_{0}$', size = 15)
plt.legend(fontsize = 12)
plt.show()
# beta_1 시각화
sns.distplot(beta_1_list, label='$\hat\u03B2_1$')
plt.vlines(x=beta_1, ymin=0, ymax=2.5, alpha = .5, colors='k', linestyles='dashed', label=f'$\u03B2_1$ = {beta_1}')
plt.vlines(x=np.mean(beta_1_list), ymin=0, ymax=2.8, alpha = .5 ,colors='r', linestyles='dotted', label=f'$\widebar\hat\u03B2_1$ = {np.mean(beta_1_list) : .3f}')
plt.title(r'$\hat \beta_{1}$의 분포도')
plt.xlabel(r'$\hat \beta_{1}$', size = 15)
plt.legend(fontsize = 12)
plt.show()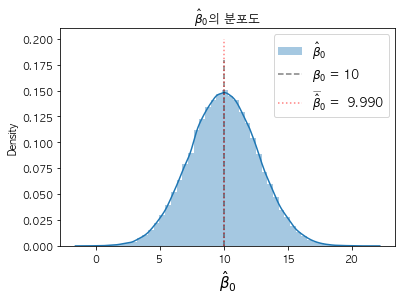
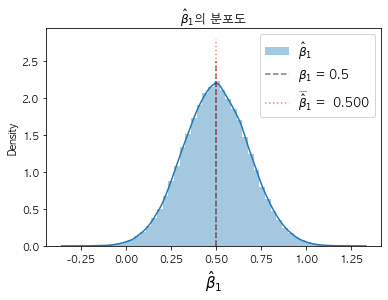
이처럼 회귀계수는 모수에 가깝게 도출되는 것을 알 수 있습니다.
'공부 > 통계학' 카테고리의 다른 글
| 선형회귀 분석2 (회귀계수) python (0) | 2022.04.01 |
|---|---|
| 선형회귀 분석1 (결정계수 구하기) python (0) | 2022.04.01 |
| 선형회귀 기초 (0) | 2022.03.24 |
| 로지스틱 회귀분석 (Logistic Regression) python (0) | 2022.02.21 |
| 일원분산분석 (One-way ANOVA) python (0) | 2022.02.15 |




댓글