정규분포, 이항분포, t분포, 카이제곱분포 등 다양한 분포가 존재한다.
이번에는 파이썬을 활용하여 각 분포에 대해 그려보도록 한다.
정규분포
# 정규분포 그리는 함수
def normal_df(N, sigma, mu):
# 라이브러리 호출
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import seaborn as sns
# 한글폰트 출력 가능 코드
from matplotlib import rc
rc('font', family='AppleGothic') # Mac Os
#rc('font', family='NanumGothic') # Windows Os
plt.rcParams['axes.unicode_minus'] = False
# 랜덤데이터 형성 (정규분포)
np.random.seed(0)
x = sp.stats.norm(mu, sigma).rvs(N)
# 시각화
ax = sns.distplot(x, kde=False, fit=sp.stats.norm, label=f"normal df (Variance :{x.std() : .3f})")
plt.legend(bbox_to_anchor=(1.0, .2))
plt.ylabel('PDF (확률밀도함수)')
plt.xlabel('X (독립변수)')
plt.show()
# 정규분포 형성 (평균 = 10, 표준편차 = 10)
normal_df(1000000, 10, 10)
# 표준정규분포 형성 (평균 = 1, 표준편차 = 1)
normal_df(1000000, 1, 1)

정규분포의 특성
- 평균, 최빈값, 중앙값이 모두 일치한다.
- X가 극단치가 되면서 점차 X축에 근접하지만, X축에 완전히 일치하진 않는다.
- 평균 값을 중심으로 좌우 대칭을 이룬다.
- 중심극한정리 (central limit theorem, CLT)로 데이터의 개수가 충분히 많은 경우, 정규분포를 따르게 된다.
- µ ±1 표준편차, 2표준편차, 3표준편차 사이의 확률밀도는 각각 68, 95, 99.7%이다. (3시그마 규칙, empirical rule, 경험적인 규칙)
- Z-score를 활용하여 신뢰수준 90, 95, 99% 구간을 구할 수 있다.
- P(µ -1.645 * STD < X < µ +1.645 * STD) = 90%
- P(µ -1.960 * STD < X < µ +1.960 * STD) = 95%
- P(µ -2.756 * STD < X < µ +2.756 * STD) = 99%
- 정규화를 통해 표준정규분포로 만들 수 있다.
이항분포
# Probability density of the binomial distribution
# P만큼의 성공확률을 갖는 n 회 시행에 대해서 k회가 성공할 확률을 도출함
def bin_dist(k, n, p):
# 필요한 라이브러리 호출
from math import factorial
nck = factorial(n) / (factorial(k) * factorial(n - k))
proba_df = nck * pow(p, k) * pow(1-p, n-k)
return proba_df
def binomial_df(k,n,p):
# 필요한 라이브러리 호출 (팩토리얼 계산을 위해 math의 factorial 매서드를 호출함)
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(k)
proba_df1 = np.array([bin_dist(k, n, p) for k in range(k)])
print(proba_df1)
# 표를 그리는 코드
plt.ylim(0, p)
plt.xlim(-1, k)
plt.bar(x, proba_df1, label = f'independent experiments : {n}\nSuccess proba for n = 1 : {p * 100}%')
plt.xlabel('independent experiments')
plt.ylabel('proba of success')
plt.legend()
plt.show()
binomial_df(16,15,0.3)
출력 결과
[4.74756151e-03 3.05200383e-02 9.15601148e-02 1.70040213e-01
2.18623131e-01 2.06130381e-01 1.47235986e-01 8.11300333e-02
3.47700143e-02 1.15900048e-02 2.98028694e-03 5.80575378e-04
8.29393397e-05 8.20279183e-06 5.02211745e-07 1.43489070e-08]
이항분포는 P만큼의 성공확률을 가지는 사건에 대해 n 회 시행했을 때, k회 성공하는 확률의 분포를 나타낸다.
가장 쉬운 예시를 보면, 동전던지기가 있을 것이다.
여기서 이항분포가 정규분포에 근사한 형태를 보이기 위해서는 확률이 0.5에 가깝고, n이 충분히 클때 가능하다고 한다.
(np, np(1-p) ** 1/2)이 두 값이 5보다 클 때, 평균이 np이고 분산이 np(1-p)인 정규분포를 따른다고 한다.
예시 코드
binomial_df(40,39,0.5)
>>>
[1.81898940e-12 7.09405867e-11 1.34787115e-09 1.66237442e-08
1.49613697e-07 1.04729588e-06 5.93467666e-06 2.79777614e-05
1.11911046e-04 3.85471380e-04 1.15641414e-03 3.04872818e-03
7.11369910e-03 1.47746058e-02 2.74385537e-02 4.57309228e-02
6.85963841e-02 9.28068727e-02 1.13430622e-01 1.25370688e-01
1.25370688e-01 1.13430622e-01 9.28068727e-02 6.85963841e-02
4.57309228e-02 2.74385537e-02 1.47746058e-02 7.11369910e-03
3.04872818e-03 1.15641414e-03 3.85471380e-04 1.11911046e-04
2.79777614e-05 5.93467666e-06 1.04729588e-06 1.49613697e-07
1.66237442e-08 1.34787115e-09 7.09405867e-11 1.81898940e-12]
베르누이 이항분포
베르누이는 시행이 1번인 이항분포라 보면된다. 즉 동전던지기를 한 경우, 성공 or 실패로 나뉘는 것이다.
베르누이 분포의 경우, X변수는 성공 or 실패만 존재하는 이산확률변수(Discrete random variable)이다.
여기서 X = 1의 성공확률은 θ이다.
X ~ Bern(θ)는 '이산확률변수 X가 모수 θ의 베르누이 분포를 따른다'를 의미한다.
이를 코드로 구현해보도록 한다.
def sim_bernoulli_df(p, n):
import seaborn as sns
from scipy.stats import bernoulli
import pandas as pd
rv = bernoulli(p)
X = rv.rvs(n, random_state=2022)
y = np.bincount(X, minlength=2)/len(X)
sns.countplot(x = X)
plt.xticks([0, 1], [f"X=0\n{int(y[0]*n)} times", f"X=1\n{int(y[1]*n)} times"])
plt.title(f"simulation of Bernoulli df ({n} times)")
plt.show()
df = pd.DataFrame({"theoretic": rv.pmf(XX), "simulation": y}).stack()
df = df.reset_index()
df.columns = ["value", "type", "ratio"]
df.pivot("value", "type", "ratio")
print(df)
sns.barplot(x="value", y="ratio", hue="type", data=df)
plt.title(f"simulation vs theoretic ({n} times)")
plt.show()
sim_bernoulli_df(0.4, 10000)먼저 1번째 표는 성공확률 θ=0.4인 베르누이 분포를 따르는 이산확률변수 X를 10000번 시행했을 때 몇번 성공한지 보여주는 표다.

그리고 다음 표는 이론적인 성공, 실패 비율과 실제 시행 결과 성공, 실패 비율을 표시한다.
value type ratio
0 0 theoretic 0.6000
1 0 simulation 0.6012
2 1 theoretic 0.4000
3 1 simulation 0.3988마지막 표는 실제 시행과 이론적 성공 비율을 표로 그린 결과다.
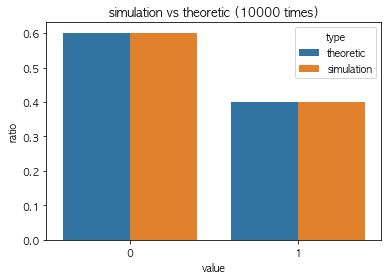
10000회 시행한 결과는 이론과 실제가 거의 유사하다고 볼 수 있다.
T-분포
1908년에 William Sealy Gosset이 "스튜던트"라는 필명으로 1908년에 발견한 분포이다. 기네스 양조 공장에서 맥주에 사용되는 보리의 질을 테스트하기 위해 분포를 도입했는데, 경쟁사에게 이런 기법을 숨기기 위해 사용했다 알려진다. 이후 Sir Ronald Aylmer Fisher가 이 분포를 Student-distribution으로 부르며 t라는 기호를 사용하게 되며 Student-t distribution으로 불리게 되었다.
t 분포의 식은 다음과 같다.
여기서 분산, 표준편차를 모르지만 구할수 있기 때문에 분산을 모르는 경우 평균을 추정할 수 있는 장점이 존재한다.
따라서 모분산을 모르는 경우 (대다수가 그러함) 모평균을 추정하는 t-test를 진행할 수 있는 것이다. (대신 여기선 표본분산을 사용한다.)
또한, t분포는 원점에 대해 대칭인 구조이다. 그리고 데이터의 수가 30을 넘을 때 정규분포에 근사하게 된다. (중심극한정리)
하지만 30개 이하인 소표본인 경우에는 t-분포를 사용하여 정규분포 대신 신뢰구간을 도출하는 것이다.
그렇다면 코드로 t분포를 그려보도록 한다.
def t_df(DF):
# 라이브러리 호출
import math
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-5, 5, 101)
y = (math.gamma((DF+1) / 2) / (math.gamma(DF / 2) * math.sqrt(math.pi * DF))) * (1 + t ** 2 / DF) ** (-(DF + 1) / 2)
plt.plot(t, y)
plt.xlabel("t")
plt.ylabel("pdf")
plt.title("t-df")
plt.legend([f"t-df (Degree of Freedom = {DF})"], bbox_to_anchor=(1, .2))
plt.show()
t_df(5)
물론 scipy 라이브러리를 활용해도 가능하다.
def t_df_stats(DF):
import scipy.stats as stats
import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(-5, 5, 101)
y1 = stats.t(DF).pdf(t)
plt.plot(t, y1)
plt.xlabel("t")
plt.ylabel("pdf")
plt.title("t-df with scipy")
plt.legend([f"t-df (Degree of Freedom = {DF})"])
plt.show()
t_df_stats(5)
카이제곱 분포
- 카이제곱 분포는 각각 독립이고 표준정규분포인 확률변수 Zi의 제곱의 합 X가 따르는 확률분포이다.
X = Z_12 + Z_22 + ... + Z_n2- 표본분산의 확률분포가 카이제곱 분포를 따른다.
- 따라서 주로 분산분석에 이용된다. (정규분포를 따르는 여러 데이터를 한번에 검정할 수 있기 때문이다)
- 표본분산으로 모분산을 추론하는 카이제곱 검정이 있다. (추가 정보)
- 비대칭적인 모양으로 자유도가 높아질수록 정규분포에 근사하게 된다

이를 코드로 구현해 보았다.
def chi2(DF):
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
X = np.linspace(0, 15, 151)
plt.plot(X, chi2(DF).pdf(X), label=f"Chi2 (Degree of Freedom = {DF})")
plt.legend()
plt.title('Chi-Square df')
plt.show()
chi2(4)
'공부 > 기초통계' 카테고리의 다른 글
| 표본과 모집단의 이해 (0) | 2022.03.21 |
|---|---|
| 오차, 잔차, 편차의 차이 (기초통계) python (0) | 2022.03.19 |
| confusion matrix (혼동행렬) python (0) | 2022.03.17 |
| 기초통계 (상관계수) python (0) | 2022.02.09 |
| 기초 통계 (분산) python (0) | 2022.02.08 |







댓글