이전 포스트에 이어서 작성하는 내용입니다.
2022.02.21 - [공부/통계학] - 로지스틱 회귀분석 (Logistic Regression) python
로지스틱 회귀분석 (Logistic Regression) python
이번에는 로지스틱 회귀분석을 시행해보겠습니다. 이 포스트에는 코드 위주로 업로드되며, 관련 이론은 다음을 참고해주세요. 2021.11.16 - [공부/통계학] - 로짓분석 로짓분석 로짓 분석을 설명하
signature95.tistory.com
혼동행렬을 모형의 정확성을 평가하는 지표로 흔히 사용됩니다.
저번 포스트 마지막에도 혼동행렬을 표시했었는데요, 이에 대해 좀 더 자세하게 공부하려 합니다.
로지스틱 회귀분석으로 특정인이 사망할 확률, 생존할 확률은 각각 p, 1-p로 구성되어 있는데, 여기서 임계치는 0.5로 설정되어 있습니다. 만약 여기서 임계치를 바꾸게 된다면 어떻게 되는지 코드를 통해 알아보며 혼동행렬에 대해 설명하려 합니다.
먼저 코드입니다.
# 혼동행렬 (confusion matrix)
cm_df = pd.DataFrame(logreg.pred_table())
cm_df.columns = ['Predicted 0', 'Predicted 1']
cm_df = cm_df.rename(index={0: 'Actual 0',1: 'Actual 1'})
cm_df
>>>
Predicted 0 Predicted 1
Actual 0 478.0 71.0
Actual 1 110.0 230.0이는 훈련데이터로 도출한 target 값에 대해 실제 얼마나 부합하는지 확인하는 것입니다.
(logreg 가 로지스틱모형 명칭입니다)
그렇다면 임계치가 0.5인 점을 알기 위해 먼저 예측한 y_pred를 봅시다.
y_pred = logreg.predict(X_train)
y_pred
>>>
0 0.088137
1 0.907371
2 0.661907
3 0.873026
4 0.111580
...
886 0.194491
887 0.885967
888 0.574308
889 0.389516
890 0.124269
Length: 889, dtype: float64
그렇다면 이번에는 임계치를 조정하여 각 확률에 따라 target을 1, 0으로 분류합니다.
def cut_off(y_pred, threshold):
y = y_pred.copy()
y[y>threshold] = 1
y[y<=threshold] = 0
return y.astype(int)
# 예측값에 대한 임계치는 0.5로 설정
y_pred = cut_off(logreg.predict(X_train),0.5)
# 실제, 예측 값에 대한 데이터 프레임 형성
df = pd.DataFrame(list(zip(Y_train, y_pred)), columns = {'actual', 'pred'})
print(df)
>>>
pred actual
0 0 0
1 1 1
2 1 1
3 1 1
4 0 0
.. ... ...
884 0 0
885 1 1
886 0 1
887 1 0
888 0 0
[889 rows x 2 columns]이를 그래프로 표현해보겠습니다.
ax = sns.countplot(x=df['pred'], hue=df['actual'])
for p in ax.patches:
height = p.get_height()
ax.text(p.get_x() + p.get_width() / 2., height + 3, height, ha = 'center', size = 9)
ax.set_title('로지스틱 회귀분석 결과와 실제값')
plt.show()
이번에는 임계치 값에 따른 평가지표까지 출력해 봅니다.
def cut_off(Y_train, Y_pred, threshold):
# 빈 리스트 생성
actual0 = []
actual1 = []
# 임계치 조정
y = Y_pred.copy()
y[y>threshold] = 1
y[y<=threshold] = 0
y.astype(int)
# 실제, 예측 값에 대한 데이터 프레임 형성
tmp = pd.DataFrame(list(zip(Y_train, y)), columns = {'actual', 'pred'})
for i in [0,1]:
for j,k in zip([0,1],[actual0,actual1]):
k.append(len(tmp.loc[(tmp.actual == i) & (tmp.pred == j)]))
# 혼동행렬 형성
confusion_matrix = pd.DataFrame(zip(actual0, actual1))
print(actual0 + actual1)
confusion_matrix.columns = ['Predicted 0', 'Predicted 1']
confusion_matrix = confusion_matrix.rename(index={0: 'Actual 0',1: 'Actual 1'})
# 평가지표 형성
precision = actual0[0]/sum(actual0)
recall = actual0[0]/(actual0[0]+actual1[0])
accuracy = (actual0[0]+actual1[1])/(sum(actual0)+sum(actual1))
f1_scroe = 2 * (precision * recall) / (precision + recall)
print(f'임계치 {threshold} 수준에서의 분류 평가 지표')
print(f'Precision (정밀도) :{precision * 100 : .2f}%')
print(f'Recall (재현율) :{recall * 100 : .2f}%')
print(f'Accuracy (정확도) :{accuracy * 100 : .2f}%')
print(f'F1 Score :{f1_scroe * 100 : .2f}%')
print(confusion_matrix,'\n')
# return confusion_matrix, actual0, actual1, precision,recall,accuracy,f1_scroe
cut_off(Y_train, logreg.predict(X_train), 0.5)
>>>
[478, 71, 110, 230]
임계치 0.5 수준에서의 분류 평가 지표
Precision (정밀도) : 87.07%
Recall (재현율) : 81.29%
Accuracy (정확도) : 79.64%
F1 Score : 84.08%
Predicted 0 Predicted 1
Actual 0 478 110
Actual 1 71 230여기서 평가지표에 대해 알아봅시다.
먼저 혼동행렬은 다음과 같이 구성됩니다.
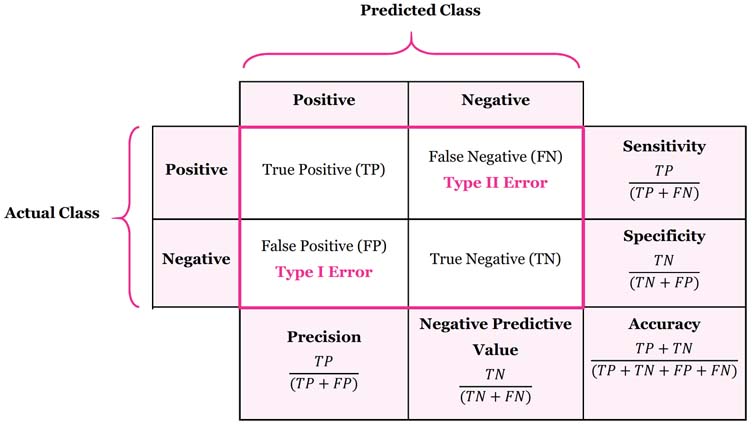
일반적으로 양성, 음성 등으로 판별되는 질병에 빗대어 많이 설명합니다
- TP : 실제 양성인 경우 (실제도 양성, 예측도 양성)
- FP : 가짜 양성인 경우 (실제는 음성, 예측이 양성 -> 예측이 틀림) : 1종 오류 (p-value, 알파값)
- FN : 가짜 음성인 경우 (실제는 양성, 예측이 음성 -> 예측이 틀림) : 2종 오류 (베타값)
- TN : 실제 음성인 경우 (실제도 음성, 예측도 음성)
여기서 True, False을 판별하는 것은 실제 값과 예측이 다른 경우를 의미하고 P, N은 예측을 어떻게 했는지에 따라 다릅니다.
이 부분이 항상 햇갈리는데요, 주의하셔야 합니다
그렇다면 각 개별지표를 알아봅시다.
보통 Accuracy(정확도), Precision (정밀도), Sensitivity(민감도 = Recall), Specificity (특이도) 등으로 표시됩니다.
정확도는 전체 중 실제와 예측이 일치한 비율을 의미합니다.
정밀도는 양성으로 예측한 것중 실제 양성이 차지하는 비중입니다.
민감도, 재현율은 실제 양성인 것 중 양성으로 예측한 것의 비중입니다.
특이도는 실제 음성인 것 중, 음성으로 예측한 것의 비중입니다.
여기서 F1 score가 있는데요, 이는 recall, precision의 조화평균입니다.
참고로 조화평균은 작은 쪽의 비중을 높은 가중치로 설정한 평균입니다.
보통 정확도가 높으면 모델이 좋다고 판단할 수 있지만, 만약 데이터의 비중에서 양성과 음성이 차지하는 비중의 차이가 매우 심한 경우에는 정확도를 모델 평가지표로 삼게 되면 오류를 범할 확률이 높습니다.
예시로 990명의 음성과 10명의 양성에서 전부 음성으로 맞춘 경우, 정확도는 99%에 육박합니다. 하지만 민감도는 0%가 되는 것이죠. 이렇기 때문에 극단적인 차이가 존재하는 데이터에서는 정확도가 아닌 정밀도, 민감도를 통해 모델의 정확성을 판단해야 합니다.
그렇다면 여기서 임계치를 조정해보며 결과 값을 비교해 보도록 합니다.
코드는 다음과 같습니다.
# 리스트 형성
precision_list = []
recall_list = []
accuracy_list = []
f1_scroe_list = []
AP_00 = []
AP_01 = []
AP_10 = []
AP_11 = []
# 임계치를 0.1~0.9까지 설정
for i in np.linspace(0.1,0.9,9):
maxtix, actual0, actual1, precision,recall,accuracy,f1_scroe = cut_off(Y_train, logreg.predict(X_train), i)
AP_00.append(actual0[0])
AP_01.append(actual0[1])
AP_10.append(actual1[0])
AP_11.append(actual1[1])
precision_list.append(precision * 100)
recall_list.append(recall* 100)
accuracy_list.append(accuracy* 100)
f1_scroe_list.append(f1_scroe* 100)
# 데이터 프레임화
score = pd.DataFrame({'AP_00' : AP_00,
'AP_01' : AP_01,
'AP_10' : AP_10,
'AP_11' : AP_11,
'precision' : precision_list,
'recall' : recall_list,
'accuracy' : accuracy_list,
'f1_score' : f1_scroe_list}).transpose()
score.columns= [f'threshold = {i}' for i in np.linspace(0.1,0.9,9)]
score결과
threshold = 0.1 threshold = 0.2 threshold = 0.3 \
AP_00 59.000000 376.000000 399.000000
AP_01 490.000000 173.000000 150.000000
AP_10 9.000000 62.000000 65.000000
AP_11 331.000000 278.000000 275.000000
precision 10.746812 68.488160 72.677596
recall 86.764706 85.844749 85.991379
accuracy 43.869516 73.565804 75.815523
f1_score 19.124797 76.190476 78.775913
threshold = 0.4 threshold = 0.5 threshold = 0.6 \
AP_00 456.000000 478.000000 492.000000
AP_01 93.000000 71.000000 57.000000
AP_10 104.000000 110.000000 119.000000
AP_11 236.000000 230.000000 221.000000
precision 83.060109 87.067395 89.617486
recall 81.428571 81.292517 80.523732
accuracy 77.840270 79.640045 80.202475
f1_score 82.236249 84.080915 84.827586
threshold = 0.7 threshold = 0.8 threshold = 0.9
AP_00 537.000000 546.000000 546.000000
AP_01 2.000000 3.000000 3.000000
AP_10 178.000000 242.000000 278.000000
AP_11 162.000000 98.000000 62.000000
precision 97.814208 99.453552 99.453552
recall 75.104895 69.289340 66.262136
accuracy 78.627672 72.440945 68.391451
f1_score 84.968354 81.675393 79.533867
'공부 > 기초통계' 카테고리의 다른 글
| 표본과 모집단의 이해 (0) | 2022.03.21 |
|---|---|
| 오차, 잔차, 편차의 차이 (기초통계) python (0) | 2022.03.19 |
| Distribution (분포도) python (0) | 2022.02.10 |
| 기초통계 (상관계수) python (0) | 2022.02.09 |
| 기초 통계 (분산) python (0) | 2022.02.08 |




댓글