ACF와 같이 확인하는 부분이 PACF이다.
간단하게 말하면 편미분을 활용하는것으로 lag = 2인 경우, lag = n을 배제하고 lag=2와 lag=0의 편미분계수를 구하는 것이다.
ACF는 앞 포스트에서 다룬 것을 참고하면 된다.
2022.01.20 - [공부/모델링] - ACF (auto-correlative function, 자기상관함수) python
ACF (auto-correlative function, 자기상관함수) python
자기상관함수는 보통 시계열 분석으로 도출된 잔차가 시간의 흐름에 따라 상관성이 존재하는지 확인하는 함수이다. 물론 ARIMA를 시행할 때, p,q를 설정하기 위해서도 ACF를 활용하기도 한다. 이번
signature95.tistory.com
데이터는 divvy_data로 계속 이어진다.
거두절미하고 바로 PACF로 넘어가자.
먼저 plot을 그리는 코드는 다음과 같다.
def pacf_plot(data, N_LAGS, pval):
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data, lags=N_LAGS, alpha=pval, method='ywm')
plt.xlabel(f'Lag at k (0 to {N_LAGS})')
plt.ylabel("lag at k's Partial autocorrelation")
plt.show()
pacf_plot(data['rides'], 22, 0.05)
먼저 X축은 lag의 개수에 따른 데이터다. 따라서 N_LAGS를 설정한 만큼 개수가 추가되는 것이며, xlabel에서도 0 to 22로 나와있는 것을 확인할 수 있다.
Y축은 lag 개수에 따른 데이터와 lag=0일때 데이터의 편미분 추정 계수이다.
파란 음영은 신뢰구간으로 alpha = 0.05 일때 95%의 신뢰구간으로 표시된 값이다.
y축에 해당하는 편미분 추정 계수는 pacf함수를 통해서도 구할 수 있다.
def pacf(data, alpha, N_LAGS):
from statsmodels.tsa.stattools import pacf
result = pd.DataFrame()
result['pacf'] = pacf(data, alpha=alpha)[0][:N_LAGS+1]
result['upper confidence interval'] = [pacf(data, alpha=alpha)[1][i][1] for i in range(N_LAGS + 1)]
result['lower confidence interval'] = [pacf(data, alpha=alpha)[1][i][0] for i in range(N_LAGS + 1)]
return result
result = pacf(rides['rides'], 0.05, 22)
print(result)
>>>
pacf upper confidence interval lower confidence interval
0 1.000000 1.000000 1.000000
1 0.858297 0.909626 0.806967
2 -0.000813 0.050516 -0.052143
3 0.293658 0.344987 0.242328
4 0.103616 0.154946 0.052286
5 0.211171 0.262501 0.159841
6 0.462841 0.514171 0.411512
7 0.295598 0.346928 0.244268
8 -0.137638 -0.086308 -0.188967
9 -0.139587 -0.088257 -0.190917
10 0.049068 0.100398 -0.002261
11 0.020440 0.071770 -0.030890
12 0.011824 0.063153 -0.039506
13 0.276852 0.328181 0.225522
14 0.158251 0.209581 0.106921
15 -0.147220 -0.095890 -0.198550
16 -0.089307 -0.037977 -0.140637
17 0.040946 0.092276 -0.010383
18 -0.009722 0.041608 -0.061052
19 0.003570 0.054900 -0.047759
20 0.151475 0.202805 0.100146
21 0.092746 0.144075 0.041416
22 -0.117050 -0.065720 -0.168380그렇다면 파란색 음영으로 표시되기도 하고 pacf함수로 구현된 신뢰구간은 어떻게 도출되는 것일까?
식은 다음과 같다.
import scipy.stats
scipy.stats.norm.ppf(1-(alpha)/2) * (1/np.sqrt(data.shape[0]))norm은 normal distribution(정규분포)을 의미한다.
그렇다면 alpha = 0.05로 설정되어 있으므로 분위수 97.5%에 위치한 정규분포의 X값을 구하면 된다.
ppf는 누적확률분포의 역함수로 그림을 그리면 다음과 같다.

누적확률분포에는 X값을 넣으면 Y값에 분위수가 출력되는데, 역누적분포함수(PPF)는 반대로 보면된다.
따라서, 위 식을 보면 97.5%에 위치한 정규분포의 X값이 도출되는 것이다. 표준정규분포 N(0,1)에서 근사값으로는 1.96이 된다.
그리고 그 값에 {1 / (데이터 개수)} ** 1/2 를 곱하면 되는 것이다.
그렇다면 이번에는 PACF Plot에 추정계수와 신뢰구간을 도출해보자.
def pacf_plot(data, N_LAGS, pval):
# 라이브러리 호출
from statsmodels.graphics.tsaplots import plot_pacf
from statsmodels.tsa.stattools import pacf
import scipy.stats
# 편자기상관계수를 구하는 부분
auto = pd.Series(data.values)
for i in range(0, N_LAGS+1):
# lag 별 pacf 추정 계수를 출력하는 부분
print(f"lag at {i}'s Partial autocorrelation = ", round(pacf(data, alpha=.05)[0][i],2))
scatter = pd.DataFrame()
scatter['lags'] = [i for i in range (1, N_LAGS +1)]
scatter['Partial autocorrelation'] = [pacf(data, alpha=.05)[0][i] for i in range(1, N_LAGS +1)]
print(f"1번째 lag애서 파란 음영의 값 범위는 -{scipy.stats.norm.ppf(1-(alpha)/2) * np.sqrt(1/(data.shape[0]-1))}, +{scipy.stats.norm.ppf(1-(alpha)/2) * np.sqrt(1/(data.shape[0]-1))}입니다.")
# 표 그리는 부분
plot_pacf(data, lags=N_LAGS, alpha=pval, method='ywm')
plt.xlabel(f'Lag at k (0 to {N_LAGS})')
plt.ylabel("lag at k's Partial autocorrelation")
# lag 별로 PACF 추정 계수를 점으로 찍는 부분
plt.scatter(x=scatter['lags'], y=scatter['Partial autocorrelation'], edgecolors='red',linewidth=1, s=200, alpha = .5)
# lag = 1 에서 신뢰구간의 upper 부분을 점으로 찍는 부분
plt.scatter(x=1, y=[scipy.stats.norm.ppf(1-(alpha)/2) * (1/np.sqrt(data.shape[0]))])
plt.show()
pacf_plot(data['rides'], 22, 0.05)
>>>
lag at 0's Partial autocorrelation = 1.0
lag at 1's Partial autocorrelation = 0.86
lag at 2's Partial autocorrelation = -0.0
lag at 3's Partial autocorrelation = 0.29
lag at 4's Partial autocorrelation = 0.1
lag at 5's Partial autocorrelation = 0.21
lag at 6's Partial autocorrelation = 0.46
lag at 7's Partial autocorrelation = 0.3
lag at 8's Partial autocorrelation = -0.14
lag at 9's Partial autocorrelation = -0.14
lag at 10's Partial autocorrelation = 0.05
lag at 11's Partial autocorrelation = 0.02
lag at 12's Partial autocorrelation = 0.01
lag at 13's Partial autocorrelation = 0.28
lag at 14's Partial autocorrelation = 0.16
lag at 15's Partial autocorrelation = -0.15
lag at 16's Partial autocorrelation = -0.09
lag at 17's Partial autocorrelation = 0.04
lag at 18's Partial autocorrelation = -0.01
lag at 19's Partial autocorrelation = 0.0
lag at 20's Partial autocorrelation = 0.15
lag at 21's Partial autocorrelation = 0.09
lag at 22's Partial autocorrelation = -0.12
1번째 lag애서 파란 음영의 값 범위는 -0.0513473831345478, +0.0513473831345478입니다.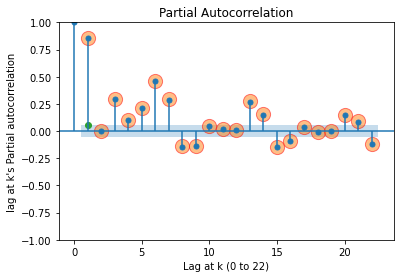
이렇게 추정계수와 신뢰구간까지 구해보았는데, lag = 2 일때 급격하게 감소하는 것을 알 수 있다.
하지만, 앞선 포스트에서 살펴보았듯 해당 데이터의 정상성은 보장되지 않는다.
따라서 이번에는 1차 차분을 한 후에 PACF를 도출해보자.
pacf_plot(diff_data, 22, 0.05)
>>>
lag at 0's Partial autocorrelation = 1.0
lag at 1's Partial autocorrelation = -0.07
lag at 2's Partial autocorrelation = -0.34
lag at 3's Partial autocorrelation = -0.14
lag at 4's Partial autocorrelation = -0.24
lag at 5's Partial autocorrelation = -0.48
lag at 6's Partial autocorrelation = -0.32
lag at 7's Partial autocorrelation = 0.12
lag at 8's Partial autocorrelation = 0.13
lag at 9's Partial autocorrelation = -0.05
lag at 10's Partial autocorrelation = -0.02
lag at 11's Partial autocorrelation = -0.01
lag at 12's Partial autocorrelation = -0.27
lag at 13's Partial autocorrelation = -0.16
lag at 14's Partial autocorrelation = 0.14
lag at 15's Partial autocorrelation = 0.09
lag at 16's Partial autocorrelation = -0.04
lag at 17's Partial autocorrelation = 0.01
lag at 18's Partial autocorrelation = -0.0
lag at 19's Partial autocorrelation = -0.15
lag at 20's Partial autocorrelation = -0.1
lag at 21's Partial autocorrelation = 0.11
lag at 22's Partial autocorrelation = 0.14
1번째 lag애서 파란 음영의 값 범위는 -0.05136501313786027, +0.05136501313786027입니다.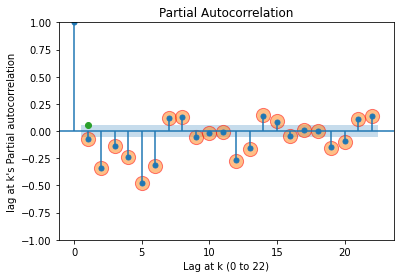
확인해보면, 9, 10, 11, 16, 17, 18 에서 신뢰구간 음영 안에 위치하는 것을 볼 수 있다.
추가)
Cross-correlation
2022.04.05 - [공부/통계학] - Cross correlation (비교상관계수) python
Cross correlation (비교상관계수) python
이전에 다룬 ACF, PACF 이후 작성하는 부분입니다. 2022.01.20 - [공부/통계학] - ACF (auto-correlative function, 자기상관함수) python ACF (auto-correlative function, 자기상관함수) python 자기상관함수는..
signature95.tistory.com
'공부 > 통계학' 카테고리의 다른 글
| 일원분산분석 (One-way ANOVA) python (0) | 2022.02.15 |
|---|---|
| 기초 통계 (중심도 이해) python (0) | 2022.02.04 |
| ACF (auto-correlative function, 자기상관함수) python (0) | 2022.01.20 |
| Differential (차분) python (2) | 2022.01.19 |
| Stationary test (정상성 검정) python (0) | 2022.01.19 |



댓글