자기상관함수는 보통 시계열 분석으로 도출된 잔차가 시간의 흐름에 따라 상관성이 존재하는지 확인하는 함수이다.
물론 ARIMA를 시행할 때, p,q를 설정하기 위해서도 ACF를 활용하기도 한다.
이번에는 자기상관성을 검정하고 이를 도표화하는 법을 알아보도록 한다.
데이터는 divvy data를 사용했으며 앞선 포스트에 이어지는 내용이기도 하다.
2022.01.19 - [공부/모델링] - Differential (차분) python
Differential (차분) python
차분을 하는 이유는 non-stationary한 데이터를 차분을 통해 stationary하게 만들어주는 것이다. 데이터를 안정화하는 작업은 제곱, 로그화, 루트, 차분이 있는데 이번에는 차분을 해볼 것이다. 정상성
signature95.tistory.com
데이터를 불러오는 부분이나, 기초 통계량을 확인하는 부분은 넘어가도록 하고 바로 ACF를 확인해본다.
def acf_plot(data, N_LAGS, alpha):
from statsmodels.graphics.tsaplots import plot_acf
fig = plot_acf(data, lags=N_LAGS, alpha=alpha)
plt.xlabel(f'Lag at 0 to {N_LAGS}')
plt.ylabel("lag at k's autocorrelation")
plt.show()
acf_plot(data['rides'], 22, 0.05)결과 출력

statsmodel에서는 lag의 개수에 따른 자기상관성을 그래프로 표시할 수 있는 매서드를 제공한다.
따라서 이를 활용해서 그래프를 그리게 되면 x축은 lag의 개수이며 y축은 lag의 개수에 따른 데이터와 상관계수를 출력한 것이다.
lag의 개수는 정상성 검정(ADF, KPSS)을 시행할 때 표시되는 used lags를 참고하여 설정하였다.
파란 음영은 alpha=0.05일때, Bartlett의 공식을 사용하여 95%의 신뢰구간으로 추정된 표준편차를 의미한다.
(참고)
MA(q)에서 q를 추정할 때 위에 나오는 자기상관계수의 추정치와 신뢰구간의 값을 비교하여 결정하는데, 만약 lag=2일때 파란 음영구간에 계수가 위치하고 있지 않지만, lag=3일때는 파란 음영 구간에 계수가 위치한다면 q=2로 설정할 수 있다.
이에 대한 논문으로 자세한 것은 링크를 참고하면 된다.
AR(p)에서 p를 추정할 때도 lag = p에서 기하급수적으로 ACF의 추정계수가 감소하거나 감소하는 패턴을 보이는 경우 p를 설정하기도 한다. 따라서 ARMA(p,q)를 추정할 수 있으며 ARIMA(p,d,q)를 추정할 때에도 이를 활용할 수 있는 것이다. (물론 d는 n차 차분을 하였을 때 시계열의 stationary를 만족하는 경우 d=n으로 설정하여 ARIMA(p,d,q)를 설정함)
다시 돌아와서 그래프 위에 파란 점은 각 lag 별 자기상관계수를 의미한다. 이를 좀더 명확하게 출력하는 함수는 다음과 같다.
def acf_plot(data, N_LAGS, pval):
from statsmodels.graphics.tsaplots import plot_acf
auto = pd.Series(data.values)
for i in range(0, N_LAGS+1):
print(f"lag at {i}'s autocorrelation = ", round(auto.autocorr(lag=i),2))
scatter = pd.DataFrame()
scatter['lags'] = [i for i in range (1, N_LAGS +1)]
scatter['autocorrelation'] = [ auto.autocorr(lag=i) for i in range(1, N_LAGS +1)]
fig = plot_acf(data, lags=N_LAGS, alpha=pval)
plt.xlabel(f'Lag at k (0 to {N_LAGS})')
plt.ylabel("lag at k's autocorrelation")
plt.scatter(x=scatter['lags'], y=scatter['autocorrelation'], edgecolors='red',linewidth=1, s=200, alpha = .5)
plt.show()
acf_plot(data['rides'], 22, 0.05)
>>>
llag at 0's autocorrelation = 1.0
lag at 1's autocorrelation = 0.86
lag at 2's autocorrelation = 0.74
lag at 3's autocorrelation = 0.71
lag at 4's autocorrelation = 0.7
lag at 5's autocorrelation = 0.71
lag at 6's autocorrelation = 0.8
lag at 7's autocorrelation = 0.87
lag at 8's autocorrelation = 0.79
lag at 9's autocorrelation = 0.7
lag at 10's autocorrelation = 0.68
lag at 11's autocorrelation = 0.67
lag at 12's autocorrelation = 0.68
lag at 13's autocorrelation = 0.78
lag at 14's autocorrelation = 0.85
lag at 15's autocorrelation = 0.77
lag at 16's autocorrelation = 0.67
lag at 17's autocorrelation = 0.66
lag at 18's autocorrelation = 0.65
lag at 19's autocorrelation = 0.66
lag at 20's autocorrelation = 0.76
lag at 21's autocorrelation = 0.82
lag at 22's autocorrelation = 0.75
그래프를 확인해본다면, 사실 자기상관계수의 추정치가 매우 높은 것을 확인할 수 있다.
또한, 파란 음영으로 표시된 95% 신뢰구간을 벗어난 수치이기 때문에 위에 있는 모든 자기상관계수의 추정치가 95%의 신뢰수준을 만족하지 못하며 5%의 통계적인 유의성을 보인다고 할 수 있다. 즉, 모든 lag의 수준에서 통계적 유의성을 찾을 수 없다는 의미가 될 것이다.
따라서 이번에는 차분을 진행한 상태의 데이터에 대해 ACF를 출력해볼 것이다.
코드는 동일하기 때문에 간단하게 확인해보겠다.
acf_plot(rides['rides'].diff(1).dropna(), 22, 0.05)
>>>
lag at 0's autocorrelation = 1.0
lag at 1's autocorrelation = -0.07
lag at 2's autocorrelation = -0.34
lag at 3's autocorrelation = -0.06
lag at 4's autocorrelation = -0.07
lag at 5's autocorrelation = -0.28
lag at 6's autocorrelation = 0.08
lag at 7's autocorrelation = 0.48
lag at 8's autocorrelation = 0.09
lag at 9's autocorrelation = -0.27
lag at 10's autocorrelation = -0.07
lag at 11's autocorrelation = -0.04
lag at 12's autocorrelation = -0.3
lag at 13's autocorrelation = 0.1
lag at 14's autocorrelation = 0.51
lag at 15's autocorrelation = 0.06
lag at 16's autocorrelation = -0.29
lag at 17's autocorrelation = -0.04
lag at 18's autocorrelation = -0.05
lag at 19's autocorrelation = -0.29
lag at 20's autocorrelation = 0.1
lag at 21's autocorrelation = 0.5
lag at 22's autocorrelation = 0.09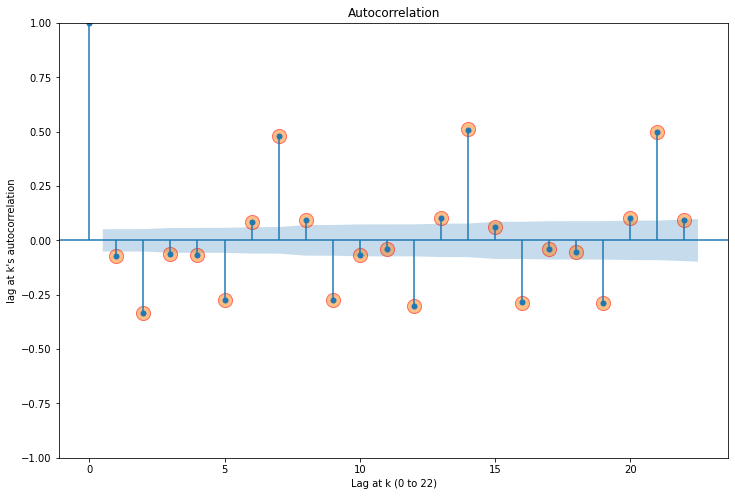
이렇게 차분을 진행하게 된다면, acf가 파란 음영에 많이 근접해 있다는 사실을 확인할 수 있을 것이다.
다음 글에서 PACF가 이어집니다.
2022.01.20 - [공부/모델링] - PACF (Partial Auto Correlation Function, 편자기상관함수) python
PACF (Partial Auto Correlation Function, 편자기상관함수) python
ACF와 같이 확인하는 부분이 PACF이다. 간단하게 말하면 편미분을 활용하는것으로 lag = 2인 경우, lag = n을 배제하고 lag=2와 lag=0의 편미분계수를 구하는 것이다. ACF는 앞 포스트에서 다룬 것을 참고
signature95.tistory.com
참고) AR모형
2022.04.06 - [공부/통계학] - AR(p) 모형
AR(p) 모형
이 포스트는 ARIMA 모형을 다루기 위한 내용으로 AR(p)에 대해 알아보고자 하여 작성하였습니다. ARIMA의 경우 먼저 p,d,q에 대해 파라미터를 지정해야 합니다. 여기서 p가 의미하는 것이 AR(p)라고 할
signature95.tistory.com
'공부 > 통계학' 카테고리의 다른 글
| 기초 통계 (중심도 이해) python (0) | 2022.02.04 |
|---|---|
| PACF (Partial Auto Correlation Function, 편자기상관함수) python (0) | 2022.01.20 |
| Differential (차분) python (2) | 2022.01.19 |
| Stationary test (정상성 검정) python (0) | 2022.01.19 |
| Stepwise Feature Selection (단계선택법) python (0) | 2022.01.14 |



댓글