Lasso Feature Selection (Embedded method) python

이전 포스트에 이어서 작성하는 내용입니다.

2022.01.14 - [공부/통계학] - Stepwise Feature Selection (단계선택법) python

Stepwise Feature Selection (단계선택법) python

2022.02.22 - [공부/머신러닝] - Ridge regression (릿지 회귀) python

Ridge regression (릿지 회귀) python

 

Reference)

 

https://medium.com/@sabarirajan.kumarappan

Sabarirajan Kumarappan – Medium

 

Lasso는 L1규제를 통해 feature간 다중공선성을 제거할 수 있는 방법으로 filter, wrapper method이외에 embedded 방법으로 feature selection이 가능한 머신러닝 기법입니다.

 

규제 식은 다음과 같습니다.

 

• N은 데이터의 개수입니다. 만약 1000개의 샘플데이터가 있다면 N=1000이 되는 것이죠.
• j는 feature의 개수입니다. 단순선형회귀인 경우에는 P=1이 되고 다중회귀에서는 P가 2이상인 값을 가집니다.
• y는 실제 target의 값입니다.
• ß는 가중치로서 OLS의 feature 계수라고 보시면 됩니다.
• 람다는 라쏘회귀의 하이퍼파라미터로 규제 강도를 의미합니다.
  • 만약 람다 = 0 이라면 OLS와 동일한 형태의 결과가 출력됩니다.
  • 만약 람다가 무한의 값이라면 아무 feature도 선택되지 않습니다.
  • 람다가 증가하면 편향성(bias)가 증가합니다. 하지만 variance는 감소합니다.

 

이런 규제를 시각화한 것이 바로 다음 그림입니다.

 

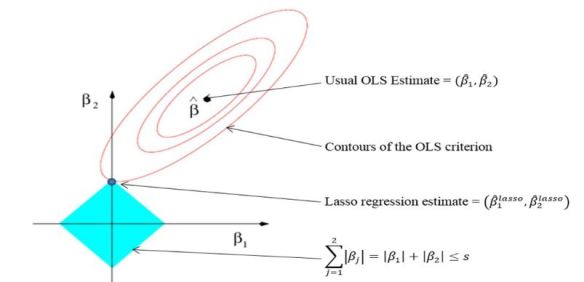
마름모 형태인 것은 바로 규제항목에 절댓값이 포함되어 있기 때문입니다. 반면 릿지 회귀는 규제항목에 절댓값이 아닌 제곱이기 때문에 원형의 형태로 그림이 도출되는 것입니다.

 

또한, 라쏘는 릿지와 다르게 feature의 가중치, 즉 회귀계수의 값을 0으로 만들어버리기 때문에 위에서 설명한 것과 같이 다중공선성을 고려한 feature selection이 가능하게 되는 것입니다.

 

이를 코드로 구현하면 다음과 같습니다. 먼저 데이터셋의 경우는 boston housing을 사용하였고 릿지 회귀를 다룬 앞선 포스트와 동일합니다.

 

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 한글폰트 출력 가능 코드
from matplotlib import rc
rc('font', family='AppleGothic') # Mac Os
#rc('font', family='NanumGothic') # Windows Os
plt.rcParams['axes.unicode_minus'] = False
from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error


# 데이터 불러오기
data = pd.read_csv("https://raw.githubusercontent.com/signature95/tistory/main/dataset/boston.csv")

# feature, target 분리
feature = data.drop(columns='MEDV')
target = data['MEDV']

# train, test 분리
X_train, X_test, Y_train, Y_test = train_test_split(feature, target, test_size = 0.2, random_state = 2022)

# 하이퍼파라미터 설정
alpha_value = 0.1
lasso = Lasso(alpha=alpha_value).fit(X_train,Y_train) 
Y_pred_train = lasso.predict(X_train) 
Y_pred = lasso.predict(X_test)

# 시각화
plt.scatter(Y_train,Y_pred_train, label = '(실제값, 예측값)', alpha=.5)
plt.plot(np.linspace(0,50,200), np.linspace(0,50,200), color = 'green', label = "45°(실제값 = 예측값)")
plt.xlabel("실제 Price: $Y_i$")
plt.ylabel("예측 Price : $\hat{Y}_i$")
plt.legend()
plt.title("예측된 Price of train set vs 실제 Price ($Y_i$ vs $\hat{Y}_i$), " + f"alpha={alpha_value}")
plt.text(y=0,x=35, s=f'MSE 값 : {mean_squared_error(Y_train,Y_pred_train) : .4f}')
plt.show()

 

 

만약 lasso에서 feature selection을 진행하고 싶다면 

 

lasso 모형을 형성한 후 coef_ 라는 항목을 넣으면 규제항목을 적용한 회귀계수 값이 도출됩니다. 

 

즉, 코드로 간단하게 예시를 보면 다음과 같습니다.

 

# 규제 강도 설정
alpha = 0.1

# 라소 모형 구축
lasso = Lasso(alpha= alpha, max_iter = 10000).fit(X_train, Y_train)

# 회귀계수가 0이 아닌 것을 True, False로 분류한 값을 원래 feature name에 넣으면 feature list 출력
feature_list = lasso.feature_names_in_[lasso.coef_ != 0]

print(feature_list)
>>>

array(['CRIM', 'ZN', 'CHAS', 'RM', 'AGE', 'DIS', 'RAD',
       'TAX', 'PTRATIO', 'B', 'LSTAT'], dtype=object)